GREPhysics.NET: GR9677 #98

GR9677 #98

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Quantum Mechanics $\Rightarrow$ }Symmetry

One recalls the simple harmonic oscillator wave functions to be symmetric about the vertical-axis (even) for the 0th energy level, symmetric about the origin (odd) for the first energy level, and so on.

If there is a wall in the middle of the well, then all the 0th energy level wave function would disappear, as would all even wave functions.

Recall the formula for SHO $E=\hbar \omega \left(n+\frac{1}{2}\right)$ . The first few odd states (the ones that remain) are $E_1 = 3/2 \hbar \omega, E_3=7/2 \hbar \omega$ , etc. This is choice (D).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

mpdude8
2012-04-20 19:35:55

Here's some "it's problem 98, it can't be that easy" logic, even if you don't see the solution right off the bat.

As long as you know the energy eigenvalues for the S.H.O. you know A, B, and E are impossible.

C would be the energy eigenvalues for the straight up S.H.O. without the wall. Let's go out on a limb and say that the wall messes up the energy states. Pretty unlikely that a giant wall in your potential wouldn't affect the energy in any way. So, I went with D.

Reply to this comment

mike
2009-11-06 17:00:34

Look at the 1992 test, problem 89...

I didn't know the ETS gave the same problems over

Reply to this comment

anmuhich
2009-04-02 12:16:25

You can also immediately eliminate all but C and D because the energy can't be zero.

segfault
2009-08-19 20:32:07

Also (C) is just the energy levels of an unperturbed harmonic oscillator, so it has to be D.

cilginfizikci
2010-03-09 02:36:30

why the energy can not be "0" ??? dont tell me that this is harmonic oscillator... coz u already change the system... ????????????

carle257
2010-04-05 19:09:54

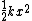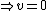If the energy were zero, then this would imply that the position is zero because the harmonic oscillator potential goes as $\frac{1}{2}kx^2$ , and the kinetic term would also have to be zero to make the total energy zero ( $\Rightarrow v=0$ ) But because of the uncertainty principle, we cannot simultaneously define the momentum and position to be zero.

Put another way, if the potential and thus position is zero, you would have a huge uncertainty in the momentum and thus the kinetic term would be non-zero.

Reply to this comment

Post A Comment!

You are replying to:

Here's some "it's problem 98, it can't be that easy" logic, even if you don't see the solution right off the bat. As long as you know the energy eigenvalues for the S.H.O. you know A, B, and E are impossible. C would be the energy eigenvalues for the straight up S.H.O. without the wall. Let's go out on a limb and say that the wall messes up the energy states. Pretty unlikely that a giant wall in your potential wouldn't affect the energy in any way. So, I went with D.

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone