|
GR9677 #96
|
|
|
|
|
Alternate Solutions |
physics_guy
2018-08-15 01:09:11 | In the center of momentum frame of the positron/electron system, their energy-momentum four-vectors sum to zero. But a single photon has nonzero energy-momentum in every reference frame. So this process would simultaneously violate energy conservation and linear momentum conservation. |  | Richard
2007-10-10 23:48:39 | I like to do it this way:
If momentum and energy are conserved in the system,
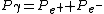
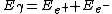 . .
But since the first particle is a photon, 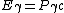 . .
This leads to, 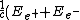= P_{e^{+}}+P_{e^{-}})
which is clearly NOT true as the energy of a particle with non-zero mass includes an additional rest energy term.
So both energy and momentum conservation cannot exist.
|  |
|
|
Comments |
physics_guy
2018-08-15 01:09:11 | In the center of momentum frame of the positron/electron system, their energy-momentum four-vectors sum to zero. But a single photon has nonzero energy-momentum in every reference frame. So this process would simultaneously violate energy conservation and linear momentum conservation.
physics_guy
2018-08-15 01:23:47 |
Clarification: the last three components of the four-vector are zero for the positron/electron system in their CM frame. The last three components of the single photon four-vector are nonzero in this frame because the photon always travels at the speed of light.
|
|  | sina2
2013-10-02 02:37:27 | This is the way I feel better. Because we don't know both electron and positron moves in same direction or not, so it's better we be careful.
Conversation of momentum:
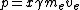
and conversation of energy:
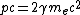
and after a few math,
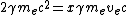
then
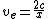
We know x maximum value could be 2, even 2 isn't satisfactory. |  | Laura
2012-11-01 07:10:41 | In nuclear physics, pair production occurs when a high energy photon interacts with a nucleus. Without a nucleus to absorb momentum, a photon decaying into electron-positron pair (or other pairs for that matter) can never conserve energy and momentum simultaneously.(The answer can be obtained without the equations)
http://en.wikipedia.org/wiki/Pair_production |  | superlaser1
2012-04-10 18:36:40 | Other than phys2718 solution I was left hanging. First consider the photon moving in the  direction. Momentum is a vector so for conservation of momentum we have the direction. Momentum is a vector so for conservation of momentum we have the 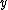 components of the particles momenta must be equal and for the components of the particles momenta must be equal and for the  momenta we have momenta we have
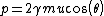)
Plugging this into the equation for conservation of energy we see
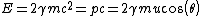 c)
So to satisfy these conservation laws we have
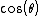=c/u)
Which can only be satisfied for 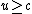 or an imaginary angle or an imaginary angle  . . |  | faith
2010-11-05 20:06:47 | confused. isnt pair production possible? i take it gammaray is some sort of a photon.
mrTrig
2010-11-07 00:40:43 |
hi faith,
Pair production certainly happens but it must be in the vicinity of a nucleus to do so. This question tells us that the photon is in free space.
Look at this nice visualization:
http://upload.wikimedia.org/wikipedia/commons/8/84/Pairproduction.png
|
|  | archard
2010-07-16 13:52:26 | Photons have spin +/- 1, electrons and positrons have spin +/- 1/2 - elimnate B and C.
Electrons and positrons have opposite charge, photons are chargeless, eliminate E.
At this point you can probably eliminate D if you know enough about particle physics. But if you're like me and do not, you can do what Yosun did and see that the electron must have velocity equal to the speed of light for both momentum and energy to be conserved.
walczyk
2011-03-06 20:28:21 |
you should analyze what your definition of conservation is.charge is conserved because the sum charge of a positron and electron is zero. Similarly you can come up with configurations of the system that don't violate momentum. What yosun did is the only solution, its not just A solution. Your solution was completely incorrect.
|
|  | torturedbabycow
2010-03-28 15:25:20 | I like Void's approach a lot, so I'm paraphrasing it as a user solution:
You can always find a reference frame where the total momentum is ZERO after the pair production - this is the rest frame of the center-of-mass of the electron and positron. However, total momentum is NEVER ZERO in any frame before the pair-production if you only have one photon.
This by itself only narrows it down to (A) or (C), so if you aren't comfortable deciding (A) yet, think of it this way. The only way to get a single "zero-momentum" photon is to have a "zero-energy" photon (zero frequency, infinite wavelength), and that's obviously a problem with Energy Conservation, not Angular Momentum conservation.
torturedbabycow
2010-03-28 15:26:44 |
Grr, and then I forgot to check "user solution." Oh well, maybe the paraphrase will help someone.
|
pam d
2011-09-21 18:19:55 |
Not sure if you're ever gonna look at this website again but this sure helped me.
|
|  | duckduck_85
2008-10-31 00:27:33 | Quicker: (E) In the decay equation shown, both charge and lep number are conserved, cross out.
(D) Strangeness? nothing to do with this. cross out
(C) and (B) Angular momentum also does not play an important role here. Cross out.
That leaves (A).
|  | a19grey2
2008-10-30 23:25:18 | I'd just like to note that the question here is very similar to question number  on this same exam. on this same exam. |  | greatm31
2008-10-25 22:33:14 | The problem is slightly more interesting than it seems. Think about it relativistically - you can only have a photon decay into an electron and a positron if it has the rest energy of the two particles: 0.511 * 2 = 1.022 MeV. BUT the energy of the photon changes based on your frame of reference (due to relativistic doppler effect). So while in one frame it has enough energy to pair-produce, in another it might not. That's why it cannot occur in a vacuum; if, on the other hand, other particles are present, they can supply the energy so that there's enough in EVERY frame. Cool, right? |  | phys2718
2008-10-14 09:56:57 | Another Solution:
Initially the energy-momentum relation for the photon is 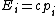 . If the pair creation could take place, then the energy-momentum relation for the electron positron pair would be . If the pair creation could take place, then the energy-momentum relation for the electron positron pair would be
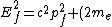^{2}c^{4}) . Now, say that momentum is conserved so that . Now, say that momentum is conserved so that 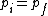 . Then from the first equation we have . Then from the first equation we have 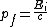 and inserting this into the second equation gives and inserting this into the second equation gives 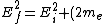^{2}c^{4}) , so if momentum is conserved then energy can't also be conserved. , so if momentum is conserved then energy can't also be conserved. |  | Richard
2007-10-10 23:48:39 | I like to do it this way:
If momentum and energy are conserved in the system,
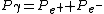
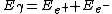 . .
But since the first particle is a photon, 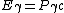 . .
This leads to, 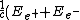= P_{e^{+}}+P_{e^{-}})
which is clearly NOT true as the energy of a particle with non-zero mass includes an additional rest energy term.
So both energy and momentum conservation cannot exist.
|  | Void
2005-11-10 07:07:43 | I think another way to look at this involves playing the reaction in reverse: pair annihilation. In the center of mass system, the total three-momentum is zero, whereas the total energy is 2E, where E is the energy of either particle. In order for three-momentum conservation, the momenta of the decay products must be conserved--thus pair annihilation yields TWO photons, both moving of course at the speed of light. So you can't have a photon of zero momentum as pointed out earlier. Four-momentum (that is, energy and three-momentum) aren't conserved.
Incidentally, this explains why in a Feynman diagram a single "electron-photon" vertex violates energy and momentum conservation. |  | daschaich
2005-11-09 00:12:48 | The momentum calculation seems to assume that the leptons are both emitted in the same direction with the same velocity. I don't believe that's correct in general.
I like to think of the limiting case where the photon's energy is exactly equal to the combined masses of the electron and positron. Then if it were to decay (it has enough energy to do so), the electron and positron would both have to be stationary, clearly violating linear momentum conservation!
Using equations, you have 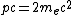 and and 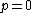 , giving , giving 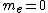 ! !
flyboy621
2010-11-06 00:02:51 |
You're saying if the photon has just enough energy to create the pair, then they can't have any kinetic energy and hence must have no momentum. But that can't be unless the photon's momentum was zero, which of course it can't be. That all makes sense for the limiting case where the photon has no excess energy.
But I don't see how that logic rules out the decay if the photon DOES have excess energy. I think you have to do the calculation or use Void's method.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
