QuantumCat
2014-09-18 14:42:35 | An alternative expression for 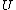 that isn't nearly as cumbersome is that isn't nearly as cumbersome is 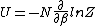 where where 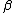 is the standard is the standard 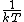 and and 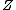 is the usual partition function. is the usual partition function. |  |
sina2
2013-10-02 02:01:11 | Because all particles are same, so, first, we find partition function for one particle.
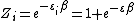
We know:
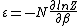
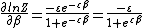
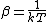 |  |
Nezumi
2013-06-22 08:48:14 | In the solution, one sees the expression:
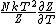 . .
Where does the 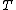 go after that? It seems to just disappear. Is this a typo? go after that? It seems to just disappear. Is this a typo?
Nezumi
2013-06-22 09:27:02 |
Ah... you get a factor of 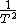 when you differentiate when you differentiate 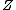 wrt wrt 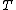 ! Silly me :) ! Silly me :)
|
|  |
wavicle
2011-10-15 13:08:50 | Maybe I missed something. I agree that as T -> 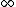 there should be equal number of particles in both states. But I disagree that, in general (or specific), we expect that as T -> 0, the internal energy to go to zero. What about a Bose-Einstein condensate? If I'm not mistaken, below the Bose temperature, all the matter is in the ground state. Doesn't this imply that said matter has the ground state energy? which is different from zero there should be equal number of particles in both states. But I disagree that, in general (or specific), we expect that as T -> 0, the internal energy to go to zero. What about a Bose-Einstein condensate? If I'm not mistaken, below the Bose temperature, all the matter is in the ground state. Doesn't this imply that said matter has the ground state energy? which is different from zero |  |
BerkeleyEric
2010-04-07 16:43:01 | I think the fastest way to do this (other than memorizing it) is to consider the high- and low-temperature limits.
At very high T each state is equally likely so we expect the energy to be (N/2)E + (N/2)0 = NE/2. This eliminates (A), (B), and (C).
At very low T we expect the energy to be zero. This eliminates (E).
timtamm
2011-08-27 11:39:52 |
i love this way of doing it... i'm just wondering if I need to memorize the formulas anyway just in case a problem can't be solved in this method... though it seems like that is unusual--- it could be useful as well
|
|  |
fjornada
2009-10-19 15:02:28 | Note: that partition function is for a single system! For N particles:
![Z=[1+e^{-\beta \epsilon}]^N](/cgi-bin/mimetex.cgi?Z=[1+e^{-\beta \epsilon}]^N)
Anyway, I also recommend solving this question by taking the high temperature limit. |  |
ramparts
2009-10-02 12:04:21 | Hmm, so I got this right without knowing what a partition function even is, lol but I forget how. I think it was something like this. Let's look at T=0: E should go to 0, of course, so we can eliminate A and E. We expect there to be some sort of  dependence, so eliminate B. Of C and D, I've seen things that look like D in the little stat mech I've done more than I've seen things like C, but I don't know how to distinguish entirely ;) But then, if you can whittle it down to two and even guess, your chances are good - gaining a whole point vs losing a quarter. dependence, so eliminate B. Of C and D, I've seen things that look like D in the little stat mech I've done more than I've seen things like C, but I don't know how to distinguish entirely ;) But then, if you can whittle it down to two and even guess, your chances are good - gaining a whole point vs losing a quarter.
I'd be curious to hear other ways of solving this without going into the full-on stat mech of it.
Tbot
2011-11-11 13:54:32 |
I think that taking the limit as T-> INFINITY narrows our options down to (D) and (E). To narrow it further, let 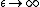 . The energy of the system should be zero (because no thermal energy will be able to excite any of subsystems). This eliminates (E), leaving (D) as the answer. Is the a correct approach? . The energy of the system should be zero (because no thermal energy will be able to excite any of subsystems). This eliminates (E), leaving (D) as the answer. Is the a correct approach?
|
|  |
a19grey2
2008-10-30 23:15:42 | Looking at the limits on T for this equation, how can D be the right answer?
As T goes to 0 the internal energy goes to infinity instead of some fixed value.
How is this possible?
schadenfraude
2008-11-02 13:40:20 |
As T goes to 0, e^(epsilon/kT) goes to infinity. Since infinity is in the denominator, the internal energy will go to zero, not infinity.
|
justguessing
2009-10-09 21:41:01 |
i've never done stat mech, but i exluded (D) cus in the limit of very high temperatures it goes to (N/2) * e ... I'd have thought that all states would be "excited" not just half of them. how do you account for that?
|
Muphrid
2009-10-10 04:42:25 |
In the high temperature limit, you can think of the two states as having roughly the same energy (that is, 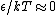 ) and thus, they're roughly equally occupied. ) and thus, they're roughly equally occupied.
Ultimately, I find Richard's explanation easiest to remember: the energy of each subsystem is just a weighted sum (energy of a state times that state's Boltzmann factor), normalized to ensure that the probabilities sum to 1.
|
|  |
tonyhong
2008-10-05 01:57:09 | what does "weakly interacting" mean? is it still valid to use the bolzman's partition function?
keradeek
2011-09-23 18:48:35 |
'weakly interacting' means that they do not affect the energy levels of one another, but they can exchange energy with each other.
|
|  |
Richard
2007-10-08 17:29:46 | Forgive me a bit of pedantry:
The partition function 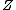 is the sum over all the Boltzmann factors is the sum over all the Boltzmann factors 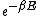 and is used to normalize the relative probability given by a single Boltzmann factor. We use it to find how many of the and is used to normalize the relative probability given by a single Boltzmann factor. We use it to find how many of the 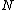 subsystems will be in the non-zero energy state: subsystems will be in the non-zero energy state:
The probability of being at the non-zero energy is:
= \frac{e^{-\beta\epsilon}}{1+e^{-\beta\epsilon})
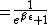
Multiply by 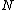 to get the total number of subsystems in the energy state, and then multiply by the energy to get the total number of subsystems in the energy state, and then multiply by the energy  to get the total energy of the system: to get the total energy of the system:
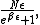
which of course is (D).
flyboy621
2010-11-05 23:40:03 |
For those who don't know, 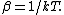 Great explanation! Great explanation!
|
|  |
antithesis
2007-10-05 07:35:53 | I believe you can do this without remembering that equation for U. If you calculate the average U for each subsystem, multiply by N, you get U.
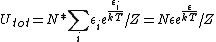 , cancel out the exponential in the numerator, and voila! , cancel out the exponential in the numerator, and voila! |  |
yosun
2005-11-21 00:49:45 | astro_allison: the Z is supposed to be in the denominator. thanks for the typo alert; the typo's been fixed. |  |
astro_allison
2005-11-17 00:36:01 | is the (dz/dt) supposed to be in the numerator or denominator? |  |
