|
GR9677 #89
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
lukenlow
2018-06-22 12:31:32 | I\'m glad that I found this useful information in such a simple explanation, this knowledge will be very useful to me 192.168.l.l |  | walczyk
2011-03-01 21:50:25 | luckily i knew the equation of radius given chord length and chord height (2l and s); everyone's tactics are so much harder, but r = s/2 + l^2/2s, so you're missing a factor of s/2 but since l >> s, its dropped by ETS. then mv^2/r = qvb is all you neat to solve it: p = qbl^2/2s + qbs/2 wooo.
timtamm
2011-08-26 20:16:59 |
this solution is rather easy... I am a big big fan... of memorizing and plugging and chugging rather than trying to figure stuff out on a high stress/ timed test. THANKS
|
nontradish
2012-04-19 20:33:54 |
I agree with timtamm to a point. I have been using Dr. Brown's flash cards from Case Western Reserve and have been able to answer many questions off the top of my head. It's better if the physics makes sense too, so you don't have to rely solely memory under pressure;) Good luck to all those taking it on Saturday and in the future!!
|
|  | kroner
2009-10-12 07:23:56 | An equivalent way to find R is to see that 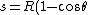) and and 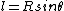 for some small angle for some small angle  . First order approximations for small . First order approximations for small  are are 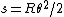 and and 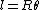 , so then , so then 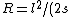) . .
aprilrussell
2018-05-30 03:48:38 |
At the very least we can eliminate choice (C) by units. \r\nhttp://fivenightsat-freddys.com
|
|  | iostream
2009-08-14 21:32:19 | easier way:
if the particle's momentum is very large, then the magnetic field's influence will be negligible - that is, it will move as if it were in a straight line. thus, the momentum should diverge as s approaches 0, from which we eliminate all choices except D and E. then, you realize the binomial approximation is never going to introduce a factor of 8, so the answer is (D). |  | askewchan
2008-11-06 19:41:29 | Also, we can eliminate (A) and (B) because we know that a larger  implies greater acceleration which means lower momentum. The same goes for a smaller implies greater acceleration which means lower momentum. The same goes for a smaller 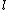 . .
In other words, if the particle has great momentum the radius of this arc will be larger, which gives a greater 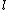 and lesser and lesser  . . |  | cordercom
2008-10-05 18:23:40 | At the very least we can eliminate choice (C) by units. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
