enterprise
2018-04-01 16:17:05 | It is just an order of magnitude calculation. escape velocity=speed of light. You can write this as 2*c=G+M-R. Every term is an order of magnitude. Take the equation and apply the logarithm on both sides. For example , M=9*10^24 so just set M=25 in the above equation. |  |
elgo
2017-10-18 03:15:42 | To get the answer exactly you need to know the Schwarzchild radius is at R=2GM. This means for there to be a blackhole, all of the mass has to be inside that radius. To convert G to general relativity units you need to divide it by 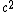 . When you put in the values for the constants, you\\\\\\\'ll get the right answer of 1cm. . When you put in the values for the constants, you\\\\\\\'ll get the right answer of 1cm. |  |
keradeek
2011-10-01 21:32:38 | well, I think the handwaving shown in the official solution is a bunch of crap, cuz energy is gamma*m*v^2, not 1/2. That's like saying the Bohr model of the atom is really informative as to what's going on, cuz it gets the right answer.
keradeek
2011-10-01 21:33:16 |
gamma*m*c^2, sorry
|
|  |
pam d
2011-09-17 19:06:43 | I think down below evanb was the only one who gave a solution that involves general relativity. The Schwarzchild radius is R = 2M (unfortunately knowing this is a combination of what courses you have taken and/or a bit of luck) in c = 1, G = 1 units. You then figure out in SI you need a factor of 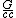 , simplify the algebra by using G = 7E-11 and M = 6E24, and arrive at about 1 cm. , simplify the algebra by using G = 7E-11 and M = 6E24, and arrive at about 1 cm.
That being said, I really like the plucky handwaving solutions. They demonstrate the type of thinking that will get you some extra points on this test. My favorite is the grape one. |  |
aqme28
2010-11-12 14:35:17 | This is a pretty poor solution, but in this case it works:
I realized the units of G are m^3/(kg*s^2)
Multiply G*M/R and you get units of (m/s)^2.
So by dimensional analysis I figured v is about the square root of GM/R
I got 4 millimeters, which is close enough to a centimeter. |  |
1234
2010-09-03 11:34:19 | Set escape velocity = c:
Escape velocity = [(2*G*M)^(1/2)]/r = c. Solve for r.
x3818919209145
2010-11-11 06:30:12 |
Doesn't the r have to go inside the square root?
|
|  |
daverbeans
2008-11-06 12:49:13 | A really quick and dirty way to do this is to consider the radius of a "stellar mass" black hole, which is about 10 solar masses. These are around 30km in radius. The sun is approximately 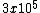 earth mass. A stellar mass black hole would then be earth mass. A stellar mass black hole would then be 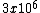 earth masses. so 30km/ earth masses. so 30km/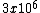 is on the order of .01m or 1cm. is on the order of .01m or 1cm.
Baharmajorana
2014-09-16 01:46:35 |
I like your solution, but we have to memorize the radius and mass of black hole!! I think the GREPHYSICS's solution is better.
|
|  |
ivalmian
2008-03-25 19:42:17 | Um, well, the reason it's called the Schwarzschild radius is that it comes from Schwarzschild's solution of Einstein's equations. Take a look:
http://en.wikipedia.org/wiki/Deriving_the_Schwarzschild_solution |  |
bat_pesso
2007-10-31 13:50:31 | i don't think relativity is such an issue here, the escape velocity depends only on the mass of the earth, not on the mass of the particle.
thus 0.5c^2 is still GM/R |  |
Jeremy
2007-10-18 13:17:00 | Not having seen such hardcore hand waving before, I would not feel comfortable with this solution even if I had thought of it. Looking in my books afterwards, I found something that's pretty cool: you can get 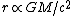 from dimensional analysis! (Of course you have to pick the right parameters.) And check this out, from dimensional analysis! (Of course you have to pick the right parameters.) And check this out, 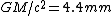 , so unless the proportionality factor is several orders of magnitude, the closest answer is (C). , so unless the proportionality factor is several orders of magnitude, the closest answer is (C).
Moral: If thou needeth formulae, consulteth dimensional analysis. I think I gave up on this problem too quickly, when I could have at least submitted an educated guess. |  |
chri5tina
2006-11-28 05:24:22 | So in all this handwaving, did he explain the 1/2?
chri5tina
2006-11-28 05:32:11 |
well, I answered my own stupid question, however I'm hitting a bug when I try to edit my above post. I get this error when I try to edit:
omg are you trying to edit someone else's comment, you phisher?! (if you're innocent, then you ought to remember to login.)
when I am already logged in. and I'm not sure where to submit bugs.
|
|  |
scottopoly
2006-11-03 19:55:34 | I once heard that if the Earth were compressed into a black hole, it would be about the size of a grape. I think that is a much faster solution. ;)
Nebula
2015-09-16 22:29:35 |
I heard marble, but still works!
|
|  |
ben
2006-11-03 15:21:30 | i've generally seen the schwarzchild radius derived from the escape velocity as shown in
http://scienceworld.wolfram.com/physics/SchwarzschildRadius.html |  |
pablojm
2006-10-28 15:30:36 | This is a good argument to convince someone who doesn't know physics, but how do you know it works...?
evanb
2008-07-01 17:22:24 |
Unfortunately, the way would know it works is by doing the general relativity. You can deduce that in the Schwarzschild metric for a point mass, any timelike or null (lightlike) trajectory (ie. any trajectory that a particle might take) that starts within R = 2M will ever wind up outside of R = 2M ( G = c = 1).
Un-unfortunately, GR reproduces lots of "Newtonian" results. You can even do most cosmology with Newtonian math. Why does that work? Because someone did it fully-general-relativistically and found that the math wound up the same...
|
|  |
