|
GR9677 #64
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
ddk1315
2014-02-09 12:23:10 | asdfuogh: 934 is the rest mass of a proton, it has nothing to do with binding energy here.
The way to answer this question is by first calculating the binding energy per nucleon in a fission reaction, which as show above is 1MeV, and then a quick look at the options available should make it obvious that the only sensible asnwer is C, as it corresponds to 200 nucleons, (D,E are certainly to small for fusion, and I have never heard of an atom that has 938 nucleons, let alone 1876!, so its not A or B either) |  | Poopiehead
2013-03-30 10:51:37 | I don't understand this problem. does the initial binding energy get converted to the binding energy of the two medium sized nuclei plus the kinetic energy of those nuclei? If thats the case the kinetic energy is -200 mev which makes no sense. |  | asdfuogh
2011-10-09 21:56:36 | I'd pick something less than 934 MeV because that's the energy you get if you had a 100% conversion of a proton. Then, I'd pick higher than 8 MeV because it's the binding energy per a nucleon.. but that reason is, well, I don't think it's very rational. But at least we get rid of two other answers! |  | Setareh
2011-10-07 14:07:00 | I didn't understand where the "0.5" came from in Yosun's equation: 2*0.5*N*8MeV/nucleon! Can anyone help me?
mets501
2011-10-09 16:31:02 |
There are two products of the decay, with each having half the number of nucleons of the original one, hence 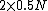 (that's what fission does). (that's what fission does).
|
|  | ticklecricket
2010-11-11 20:46:43 | Who gets to decide what is heavy and what is medium-weight? |  | testtest
2010-09-20 11:32:42 | Why is the final state particles have *higher* total binding energy after fission than the original neucleus???
pkamal
2010-10-02 20:46:18 |
The final binding energy is indeed smaller. Its the final binding energy/nucleon that's higher.
|
|  | petr1243
2008-02-16 21:28:31 | Q=(# of nucleons)(|change in energy per nucleon|)rnrnUsing the mass number of a heavy nucleon(A=200)rnrnQ = (200)(8-7)Mev = 200Mev
grace
2010-11-07 18:29:56 |
I agree with you
|
|  | relain
2007-10-31 10:19:08 | also it might help to remember that iron is the most stable nucleus with A ~ 50 and then uranium is about 250 (232, 252 whatever) so then if this is a large unstable nucleus, and each nucleon gves 1mev you're gonna get about 200... |  | Void
2005-11-10 06:49:25 | I've seen this number (200 MeV/fission) appear in a lot of elementary physics books and even a lot of lectures. If you forget everything else, just remember 200 MeV per fission... |  |
|
| Post A Comment! |
You are replying to:
asdfuogh: 934 is the rest mass of a proton, it has nothing to do with binding energy here.
The way to answer this question is by first calculating the binding energy per nucleon in a fission reaction, which as show above is 1MeV, and then a quick look at the options available should make it obvious that the only sensible asnwer is C, as it corresponds to 200 nucleons, (D,E are certainly to small for fusion, and I have never heard of an atom that has 938 nucleons, let alone 1876!, so its not A or B either)
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
