|
GR9677 #5
|
|
|
|
|
Alternate Solutions |
superPOOPERscooper
2013-10-17 08:50:18 | I honestly think the tires are the most confusing part of this problem. There are two forces acting on the car: the drag force of air, indicated as such in the diagram, and the centripetal force, indicated by 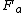 in the diagram. Remember that centripetal force in the diagram. Remember that centripetal force 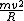 \emph{only} dictates the numerical value of the force -- it does NOT indicate which agency provides the force! In this light, we could replace the "tires" by anything: a string (where the tension would provide the centripetal force), a planet (where gravitation provides the centripetal force), or even a charged particle in a magnetic field (where Lorentz provides the centripetal force). Anyway, adding \emph{only} dictates the numerical value of the force -- it does NOT indicate which agency provides the force! In this light, we could replace the "tires" by anything: a string (where the tension would provide the centripetal force), a planet (where gravitation provides the centripetal force), or even a charged particle in a magnetic field (where Lorentz provides the centripetal force). Anyway, adding 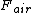 to to 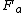 gives choice B. gives choice B. |  | 99percent
2008-11-06 06:20:59 | Centripetal force is in the direction 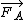
Tires exert a force in the backward direction so that the car moves in the forward direction - By Newton's third law (Action-Reaction) - The road exerts an equal force in the forward direction, i.e., 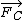
the resultant of 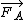 and and 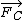 will be in the direction will be in the direction 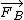
Bingo..!! |  |
|
|
Comments |
fredluis
2019-08-08 06:57:09 | I thought I could get to see and discuss all released GRE questions in here, but I can only see discussions about the four old question papers. tile contractor |  | enterprise
2018-04-01 13:56:41 | Well , The total resultant force on the car is in the radial direction. Obviously you have a drag force backwards. You should ask , What should be the direction of the force such that when you add it to the drag force , you will get the resultant centripetal force ? Obviously , Only , F_B has a direction such that it\\\\\\\'s tangent component must cancel out with the the F_air , so that the only force that survives is in the radial direction. The tangential force must cancel out so that the speed is uniform. Otherwise , you will have a torque and angular momentum will change. |  | superPOOPERscooper
2013-10-17 08:50:18 | I honestly think the tires are the most confusing part of this problem. There are two forces acting on the car: the drag force of air, indicated as such in the diagram, and the centripetal force, indicated by 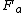 in the diagram. Remember that centripetal force in the diagram. Remember that centripetal force 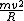 \emph{only} dictates the numerical value of the force -- it does NOT indicate which agency provides the force! In this light, we could replace the "tires" by anything: a string (where the tension would provide the centripetal force), a planet (where gravitation provides the centripetal force), or even a charged particle in a magnetic field (where Lorentz provides the centripetal force). Anyway, adding \emph{only} dictates the numerical value of the force -- it does NOT indicate which agency provides the force! In this light, we could replace the "tires" by anything: a string (where the tension would provide the centripetal force), a planet (where gravitation provides the centripetal force), or even a charged particle in a magnetic field (where Lorentz provides the centripetal force). Anyway, adding 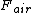 to to 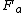 gives choice B. gives choice B. |  | sina2
2013-09-21 06:06:44 | This is the way I figure out the correct answer. I think 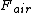 has nothing to do with the force applied by the road to the tires. The car moves forward at the moment, we know the velocity is zero in point tires touch the road, hence tires make a has nothing to do with the force applied by the road to the tires. The car moves forward at the moment, we know the velocity is zero in point tires touch the road, hence tires make a 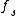 to the road in backward and oppositely, the road applies the same force at the forward to the tires. There's just another force we should think about it. In a rainy day, in defile of road, why we should reduce the speed, because it's possible we're thrown away of road toward outside. So, there is a centripetal force that keeps the car moving. So we have to the road in backward and oppositely, the road applies the same force at the forward to the tires. There's just another force we should think about it. In a rainy day, in defile of road, why we should reduce the speed, because it's possible we're thrown away of road toward outside. So, there is a centripetal force that keeps the car moving. So we have 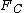 and and 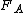 and the result force would be and the result force would be 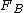 . . |  | tsharky87
2009-11-04 23:40:25 | It seems to me that if we assume the car is back-wheel driven, then the force of the road on the back tires will be 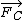 , and the force of the road on the front tires (which must be turned to the right) would be , and the force of the road on the front tires (which must be turned to the right) would be 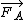 . So the driving tires are what makes it go forward and the turning tires are what pulls it toward the center, which makes sense. The resulting force of these is obviously . So the driving tires are what makes it go forward and the turning tires are what pulls it toward the center, which makes sense. The resulting force of these is obviously 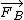 . .
But if we assume the car is front-wheel drive, then the back wheels are doing nothing but holding up the car, and the front wheels are the only force. Since the wheels must be turned to the right, the road is pushing the front wheels along where they are directed, 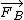 . .
I don't like this problem much and I got it wrong but that's just some insight that occurred to me. |  | Albert
2009-10-21 15:12:32 | Thank you Yosun, for this wonderful site, I am learning a great deal! |  | 99percent
2008-11-06 06:20:59 | Centripetal force is in the direction 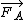
Tires exert a force in the backward direction so that the car moves in the forward direction - By Newton's third law (Action-Reaction) - The road exerts an equal force in the forward direction, i.e., 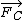
the resultant of 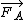 and and 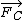 will be in the direction will be in the direction 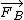
Bingo..!!
jmason86
2009-09-30 17:09:55 |
You said "The road exerts an equal force in the forward direction Fc".
The problem asks for "the horizontal force of the road on the car's tires."
It seems like by this logic, you should just go with (C). This isn't the right answer though...
|
pam d
2011-09-11 17:36:13 |
Just to be clear, you are implying here that the answer is B right?
|
postal1248
2013-10-03 16:37:51 |
I believe that by "horizontal" ETS means not the normal force, so technically all the forces in the diagram are horizontal because they lie in the horizontal plane. So the net horizontal force would be given by choice (B).
|
|  | isina
2008-10-16 14:45:53 | I do not completely agree with the answer on the grounds that it is not the only solution. Even if there is no wind force there is still force in +x direction. The reason that there is forward friction force is as follows: as the car moves in +x direction, its tires rotate in the reverse direction (at the point of contact their velocity vector points -x). So the friction of the road on the tires is actually to the opposite direction of the cars tires movement and on the same direction as the movement of the car. This results in a +x directed friction (hence the car moves).
fpaslan
2011-10-12 07:21:47 |
But the velocity of the tires at the contact point is zero. So it is again static friction which prevents the tires from sliding like FA
|
|  | evanb
2008-06-30 11:50:46 | Just a small typo: you need braces for 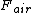 so that it doesn't look like so that it doesn't look like  |  | yosun
2005-11-10 02:00:50 | BWHB: thanks for the typo-alert; it has been corrected.
bcomnes
2011-10-09 17:57:55 |
Not in the PDF! I couldn't figure out what I was doing wrong! Apparently nothing.
|
|  | BWHB
2005-11-10 01:38:49 | All the work is right but the answer is wrong. It's FB. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
