|
GR9677 #23
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics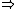 }Stability of Orbits }Stability of Orbits
The gravitational force suspect to a bit of perturbation is given as 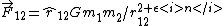 . .
One can narrow down most choices by recalling some basic facts from central force theory:
(A) No mention is made of frictional effects, and thus energy should be conserved.
(B) Angular momentum is always conserved since the net torque is 0 (to wit: the force and moment arm are parallel).
(C) This is just Kepler's Third Law applied to this force. (Recall the following bromide: The square of the period is equal to the cube of the radius---for the inverse square law force. For a perturbed force, the bromide becomes: The square of the period is equal to the 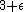 power of the radius.) power of the radius.)
(D) Recall Bertrand's Theorem from Goldstein. Stable non-circular orbits can only occur for the simple harmonic potential and the inverse-square law force. This is of neither form, and thus this choice is FALSE.
(E) Circular orbits exist for basically all potentials. A stationary orbit exists if and only if the following conditions are satisfied:  . Recall that the potential is related to the force by . Recall that the potential is related to the force by 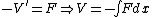 . Use . Use 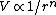 , and recalling the extra term added to the effective potential to be , and recalling the extra term added to the effective potential to be ) , one chunks out the derivatives to get the condition that , one chunks out the derivatives to get the condition that 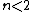 , as a potential exponent, ( , as a potential exponent, (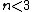 , as a force exponent) for stable orbit. One can remember this result or re-derive it whenever necessary. For , as a force exponent) for stable orbit. One can remember this result or re-derive it whenever necessary. For  , (the power exponent of the force equation), a stable circular orbit exists. Since , (the power exponent of the force equation), a stable circular orbit exists. Since  is presumably less than 1, the planet does, indeed, move in a stationary circular orbit about the sun. is presumably less than 1, the planet does, indeed, move in a stationary circular orbit about the sun.
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
tweetiebird
2014-11-24 21:09:21 | Is there a typo in the original answer for (C)? Should it be (2+e)/2 instead of (3+e)/2
?
tweetiebird
2014-11-24 21:10:50 |
Never mind. I forgot kepler's law. T^2 = kd^3
|
|  | cczako
2013-10-17 18:09:04 | The way that I solved this problem is that if only one could be false so it had to be D or E. And if C is true then (circular orbits) D must be false. |  | kaic
2013-10-15 11:17:44 | the simplest way to answer this question is to know that no elliptical orbit can be stationary: elliptic orbits always precess, as demonstrated in this nice picture
http://en.wikipedia.org/wiki/File:Precessing_Kepler_orbit_280frames_e0.6_smaller.gif |  | r10101
2007-10-30 17:03:27 | So... (D) or (E)? And why?
r10101
2007-10-30 20:35:40 |
Oops, scratch that.
|
|  | mhas035
2007-03-21 21:44:37 | Has anyone else got a paper that says that D is the right answer?
hamood
2007-04-09 11:59:45 |
yes..you can download the original exams from http://www.physics.ohio-state.edu/undergrad/ugs_gre.php
|
k93
2008-03-29 23:25:05 |
then why does the answer have E as the right not D like in the solutions to the test posted
|
dogsandfrogs
2009-10-07 13:54:34 |
Remember, the question asks which statement is FALSE. D is false, as Yosun says, so D is the answer.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
