|
GR9677 #21
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Moment of Inertia }Moment of Inertia
To solve this problem, one should remember the parallel axis equation to calculate the moment of inertia about one end of the hoop:
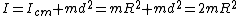 , ,
where 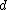 is the distance from the pivot point to the center of mass, which in this problem, is just equal to is the distance from the pivot point to the center of mass, which in this problem, is just equal to 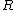 . (In the last equality, note that the moment of inertia of a hoop of radius R and mass m about its center of mass is just . (In the last equality, note that the moment of inertia of a hoop of radius R and mass m about its center of mass is just 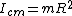 .) .)
The problem gives the period of a physical pendulum as 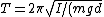}) . Thus, plugging in the above result for the moment of inertia, one has, . Thus, plugging in the above result for the moment of inertia, one has, 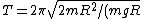}=2\pi \sqrt{2R/(g)} \approx 2*3\sqrt{2*0.2/(10)}= 12/10=1.2s) , which is closest to choice (C). (Since , which is closest to choice (C). (Since  was rounded to 3, the period should be slightly longer than 1.2s.) was rounded to 3, the period should be slightly longer than 1.2s.)
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Inune
2011-11-07 21:35:46 | I was a fan of how ETS gives a table with listed I values for a sphere, rod, and disc.... then immediately gave a problem requiring the moment of a hoop. I guess one could argue that we're just supposed to have I's memorized for common configurations, but if that's the case, why bother giving us the limited table they did in the first place.
Made me laugh.
Bumpeig
2012-08-08 11:05:11 |
Yeah I agree, it is somewhat silly. But, one already should know that I = 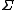 m m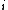 r r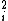 and with a circular hoop where all the mass is at r it has to be simply mr and with a circular hoop where all the mass is at r it has to be simply mr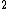 . They did choose the easiest object for not telling you what I is. . They did choose the easiest object for not telling you what I is.
I'd be a little more upset if the object wasn't so simple.
|
justin_l
2012-11-07 00:51:24 |
well...if there's any I you can do the integral for in 5 seconds...it's that of a hoop.
|
|  | Goddar
2009-10-08 10:39:29 | as far as i can tell, this result is correct only for an oscillation along the vertical axis; if we take the oscillation to be about the horizontal axis (as if a bird were swinging on the hoop), it seems after a quick calculation that (B) is closer to the answer, since the moment of inertia is not the same (perpendicular axis theorem)...
correct me if i'm wrong
fearmyplectrum
2009-10-09 16:05:14 |
I think that's why they specify the nail is on a barn wall... the wall restricts the hoop from oscillating in the horizontal axis.
|
|  | furlong
2009-08-12 19:50:59 | How come you cant just treat the hoop like a point mass at the center of the hoop oscillating from the nail at a distance R?
dstahlke
2009-10-08 20:42:00 |
Because the hoop has a nonzero moment of intertia, and a point doesn't. When the thing is swinging it has extra angular momentum due to the moment of intertia of the hoop.
|
|  | petr1243
2008-04-10 17:11:33 | no need for parallel axis theorem, just know I for the hoop and you are fine, then use d = 2r.
nobel
2008-11-03 20:43:56 |
hatt
|
carle257
2010-04-04 19:46:02 |
What motivation do you have for using d=2r? It also doesn't work out. You must have multiplied by d instead of divided because your answer would yeild ~.6 using d=2R. The moment of inertia about about the edge of the hoop is 2mR^2 as yosun correctly calculated, and that is the correct way to go about the problem.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
