|
GR9277 #85
|
|
|
|
|
Alternate Solutions |
unoriginal5279
2007-04-11 09:24:43 | When short on time (as I always am) I try to avoid calculations whenever possible. If you remember that E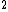 = m = m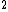 c c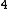 + (p c) + (p c)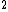 then you already know that the momentum must be less than the energy, but greater than the difference between the energy and m c then you already know that the momentum must be less than the energy, but greater than the difference between the energy and m c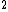 . This eliminates all but the correct answer. . This eliminates all but the correct answer. |  | Andresito
2006-03-29 15:15:31 | You could always use the general equation,
E^2 = (p*c)^2 + (m*c^2)^2
Solve for p having E = 3/2, and m*c^2 = 1/2
to obtain 1.4 as in (C).
Andresito
2006-03-29 15:21:28 |
The equation I describe is beter to use since you only ned to take a square root once, and that helps when having larger numbers, see in test 9277 problem 70.
|
Andresito
2006-03-29 15:24:03 |
The equation I describe is beter to use since you only ned to take a square root once, and that helps when having larger numbers, see in test 9277 problem 70.
|
|  |
|
|
Comments |
EPdropout
2012-11-08 17:12:29 | I used T=p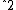 /2m=( /2m=(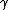 -1)mc -1)mc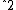 , after finding , after finding 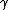 =3 =3
=>p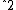 =2m*(2/3)E =2m*(2/3)E
=>p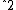 =2.0 (MeV^2/c^2) =2.0 (MeV^2/c^2)
=>p =1.4 MeV/c |  | rrfan
2011-11-06 17:41:09 | A useful shortcut on these types of relativity problems:
The solution to 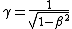 is the following: is the following: 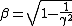 . .
Even if you don't memorize this, it is straightforward to derive and is often useful on multiple problems, saving some time on the algebra. |  | dinoco
2010-11-07 07:52:37 | You say that "v=2c/3." But since  =8/9 then =8/9 then
v should be 2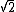 c/3 c/3 |  | unoriginal5279
2007-04-11 09:24:43 | When short on time (as I always am) I try to avoid calculations whenever possible. If you remember that E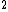 = m = m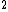 c c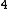 + (p c) + (p c)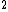 then you already know that the momentum must be less than the energy, but greater than the difference between the energy and m c then you already know that the momentum must be less than the energy, but greater than the difference between the energy and m c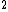 . This eliminates all but the correct answer. . This eliminates all but the correct answer.
apr2010
2010-04-08 12:25:33 |
Remarkable
|
thinkexist
2012-10-12 09:29:49 |
This is actually so simple and brilliant I cannot believe I have not thought of this before.
|
justin_l
2013-10-15 23:50:31 |
if something is remarkably brilliant, would it not be more surprising that you *do* think of it?
|
|  | Andresito
2006-03-29 15:15:31 | You could always use the general equation,
E^2 = (p*c)^2 + (m*c^2)^2
Solve for p having E = 3/2, and m*c^2 = 1/2
to obtain 1.4 as in (C).
Andresito
2006-03-29 15:21:28 |
The equation I describe is beter to use since you only ned to take a square root once, and that helps when having larger numbers, see in test 9277 problem 70.
|
Andresito
2006-03-29 15:24:03 |
The equation I describe is beter to use since you only ned to take a square root once, and that helps when having larger numbers, see in test 9277 problem 70.
|
ramparts
2009-08-06 22:54:12 |
Well, it's better to use in problem 70, but I think it's pretty clear that for this question, the E^2 equation takes a lot less calculation than the "official" answer.
|
GREview
2009-08-30 19:22:53 |
It may simplify things to not even think about the  's: 's:

Plugging 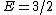 and and 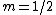 , we can solve for , we can solve for 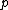 . .
|
Albert
2009-11-05 00:32:16 |
Hey, I see what you did there, you used the c's in the denominator of the units right along side the values, smart work. Best solution!
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
