GREPhysics.NET
GR | #
<< Previous | Next >>
Login | Register
   
  GR9277 #70
Problem
GREPhysics.NET Official Solution    Alternate Solutions
\prob{70}
A monoenergetic beam consists of unstable particles with total energies 100 times their rest energy. If the particles have rest mass m, their momentum is most nearly

  1. mc
  2. 10mc
  3. 70mc
  4. 100mc
  5. $10^4$ mc
Special Relativity}Gamma

E=\gamma mc^2 = 100mc^2, where ETS supplies the total energy to be 100 times the rest energy. Thus, p=\gamma mv = 100 mv, but since \gamma = 100 = \frac{1}{1-\beta^2}, where \beta=v/c, one has v\rightarrow c, as in choice (D).

See below for user comments and alternate solutions! See below for user comments and alternate solutions!
Alternate Solutions
evanb
2008-06-25 12:47:47		A way to do Andresito's method without math.

With a 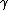\gamma of 100, the thing is definitely ultra-relativistic, meaning that it could effectively be treated as an almost-zero-mass particle.

Photons have p = E/c, so this particle should have approximately p = E / c = 100 m c		Alternate Solution - Unverified
Andresito
2006-03-29 08:48:14		E^2 = (p*c)^2 + (m*c^2)^2

let E = 100 m*c^2

solve for p to obtain p = 100 m*c
Andresito
2006-03-29 08:51:39		 E^2 = (p*c)^2 + (m*c^2)^2

let E = 100 m*c^2

since E^2 >> (mc)^2, (p*c)^2 = E^2

solve for p to obtain p = 100 m*c
Alternate Solution - Unverified
Comments
createdestroy
2013-09-18 19:16:22		E_tot = 100*E_rest
E_rest = m_0 * c^2

m_0 is given as m

E_rest = mc^2
E_tot = 100*E_rest = 100mc^2		NEC
matweiss
2010-09-16 16:00:11		This question is more straight forward than it seems.

The gamma factor is what is causes the relativistic energy to be 100 times greater than the rest energy.

This same gamma factor is what influences the momentum

Thus the relativistic energy factor of 100 will apply to the relativistic momentum factor in the exact same way

therefore, the answer is D)		NEC
engageengage
2009-01-16 18:26:19		this is a quick one once you realize that this is a 'highly relativistic' particle, since its energy by far surpasses its rest energy. Highly relativistic particles are like photons in that their energy is given by

E = pc

From this, one immediately gets the answer.
his dudeness
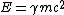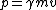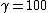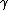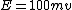2010-09-04 19:24:04		 In a similar vein, we can just use the two equations E=\gamma mc^2 and p=\gamma mv. From the first equation, we get \gamma =100. This crazy value of \gamma tells us that v is essentially equal to c, so the second equation becomes E=100mv.
his dudeness
2010-09-04 19:26:17		 I meant to write 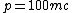p=100mc there at the end... This site is awesome in every way, but I wish there was a way to edit posts...
NEC
astrodoo
2008-10-09 07:48:15		I always appreciate your endeavor, Yosun.
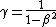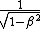In this page, you got a some typo that \gamma = \frac{1}{1- \beta^2}. It should be \frac{1}{\sqrt{1- \beta^2}}.

Anyway, thank you.		NEC
evanb
2008-06-25 12:47:47		A way to do Andresito's method without math.

With a 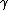\gamma of 100, the thing is definitely ultra-relativistic, meaning that it could effectively be treated as an almost-zero-mass particle.

Photons have p = E/c, so this particle should have approximately p = E / c = 100 m c		Alternate Solution - Unverified
Ning Bao
2008-01-29 12:37:57		An easier way is to use units where c=1: then E^2=p^2+m^2, and it's clear that p should be about 100m in those units, which matches the correct answer.NEC
Jeremy
2007-11-01 15:49:13		My experience has been that solutions are more quickly obtained in problems involving relativity if you AVOID GAMMA, as it can lead to lengthy algebra. Sometimes you have no choice, but this is not one of those times. Well done, Andresito.NEC
craklyn
2007-10-25 00:41:33		Thanks for the correct explanation AndresitoNEC
Andresito
2006-03-29 08:48:14		E^2 = (p*c)^2 + (m*c^2)^2

let E = 100 m*c^2

solve for p to obtain p = 100 m*c
Andresito
2006-03-29 08:51:39		 E^2 = (p*c)^2 + (m*c^2)^2

let E = 100 m*c^2

since E^2 >> (mc)^2, (p*c)^2 = E^2

solve for p to obtain p = 100 m*c
Alternate Solution - Unverified

Post A Comment!
You are replying to:
I always appreciate your endeavor, Yosun. In this page, you got a some typo that \gamma = \frac{1}{1- \beta^2}. It should be \frac{1}{\sqrt{1- \beta^2}}. Anyway, thank you.

Username:
Password:
Click here to register.
This comment is best classified as a: (mouseover)
 
Mouseover the respective type above for an explanation of each type.

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces .
type this... to get...
$\int_0^\infty$
$\partial$
$\Rightarrow$
$\ddot{x},\dot{x}$
$\sqrt{z}$
$\langle my \rangle$
$\left( abacadabra \right)_{me}$
$\vec{E}$
$\frac{a}{b}$
 
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

© 2005-2007 by Yosun Chang, All rights reserved.

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.