|
GR9277 #48
|
|
|
|
|
Alternate Solutions |
LF
2015-10-16 02:47:49 | It\'s possible to guess the answer even without knowing anything about error analysis. \r\n\r\nThere should be nothing special about the equation F = ma, so a priori, there should be no restriction on m or a being negative. However, the standard deviation is always positive. With these two observations we eliminate A, B and E:\r\n\r\nA is eliminated because if m or a are negative, then F (=ma) is negative. However option A is always positive, so sigma_F/F = [something positive] -> sigma_F must be negative, something that\'s not possible.\r\n\r\nB is eliminated because if both a and m are negative, then we have a negative number within the square root and the standard deviation can\'t be imaginary.\r\n\r\nE is eliminated because if m is negative and really large, while a is positive and really small, then the second term dominates the first and we have a positive sum. But F (=ma) is again negative, so sigma_F is again negative, and that is impossible.\r\n\r\nThat leaves C and D. Now we can use another observation: if we can measure either m or a with infinite precision, then its standard deviation would be zero. However because of the other variable, we do not know F with infinite precision, and therefore sigma_F is not zero. Plugging in this condition eliminates D, leaving C as the only possible answer. |  |
|
|
Comments |
LF
2015-10-16 02:47:49 | It\'s possible to guess the answer even without knowing anything about error analysis. \r\n\r\nThere should be nothing special about the equation F = ma, so a priori, there should be no restriction on m or a being negative. However, the standard deviation is always positive. With these two observations we eliminate A, B and E:\r\n\r\nA is eliminated because if m or a are negative, then F (=ma) is negative. However option A is always positive, so sigma_F/F = [something positive] -> sigma_F must be negative, something that\'s not possible.\r\n\r\nB is eliminated because if both a and m are negative, then we have a negative number within the square root and the standard deviation can\'t be imaginary.\r\n\r\nE is eliminated because if m is negative and really large, while a is positive and really small, then the second term dominates the first and we have a positive sum. But F (=ma) is again negative, so sigma_F is again negative, and that is impossible.\r\n\r\nThat leaves C and D. Now we can use another observation: if we can measure either m or a with infinite precision, then its standard deviation would be zero. However because of the other variable, we do not know F with infinite precision, and therefore sigma_F is not zero. Plugging in this condition eliminates D, leaving C as the only possible answer.
LF
2015-10-16 03:46:36 |
Attempting to fix the broken code. It looks OK in the preview, hope it displays right as well.\r\n---\r\nIt\'s possible to guess the answer even without knowing anything about error analysis. \r\n\r\nThere should be nothing special about the equation F = ma, so a priori, there should be no restriction on m or a being negative. However, the standard deviation is always positive. With these two observations we eliminate A, B and E:\r\n\r\nA is eliminated because if m or a are negative, then F (=ma) is negative. However option A is always positive, so ![\\sigma_{F}/F = [something positive]](/cgi-bin/mimetex.cgi?\\sigma_{F}/F = [something positive]) -> -> 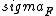 must be negative, something that\'s not possible.\r\n\r\nB is eliminated because if both a and m are negative, then we have a negative number within the square root and the standard deviation can\'t be imaginary.\r\n\r\nE is eliminated because if m is negative and really large, while a is positive and really small, then the second term dominates the first and we have a positive sum. But F (=ma) is again negative, so must be negative, something that\'s not possible.\r\n\r\nB is eliminated because if both a and m are negative, then we have a negative number within the square root and the standard deviation can\'t be imaginary.\r\n\r\nE is eliminated because if m is negative and really large, while a is positive and really small, then the second term dominates the first and we have a positive sum. But F (=ma) is again negative, so 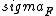 is again negative, and that is impossible.\r\n\r\nThat leaves C and D. Now we can use another observation: if we can measure either m or a with infinite precision, then its standard deviation would be zero. However because of the other variable, we do not know F with infinite precision, and therefore is again negative, and that is impossible.\r\n\r\nThat leaves C and D. Now we can use another observation: if we can measure either m or a with infinite precision, then its standard deviation would be zero. However because of the other variable, we do not know F with infinite precision, and therefore 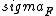 is not zero. Plugging in this condition eliminates D, leaving C as the only possible answer. is not zero. Plugging in this condition eliminates D, leaving C as the only possible answer.
|
|  | MuffinSpawn
2009-09-24 18:57:56 | If you don't remember the product rule, you can always derive it quickly using the general function rule:
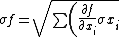^2}) |  | petr1243
2008-03-09 18:13:35 | Just a simple application of the general rules from error analysis:
For A = B +/- C :
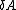 = = ^2 + (\delta C)^2})
For A = B*C or A = B/C:
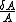 = = ^2 + (\frac{\delta A }{A})^2})
Just treat  as our as our 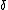
note
2008-08-21 23:12:47 |
There's a typo in your last equation, I think you meant dC/C
|
|  |
|
| Post A Comment! |
You are replying to:
It\'s possible to guess the answer even without knowing anything about error analysis. \r\n\r\nThere should be nothing special about the equation F = ma, so a priori, there should be no restriction on m or a being negative. However, the standard deviation is always positive. With these two observations we eliminate A, B and E:\r\n\r\nA is eliminated because if m or a are negative, then F (=ma) is negative. However option A is always positive, so sigma_F/F = [something positive] -> sigma_F must be negative, something that\'s not possible.\r\n\r\nB is eliminated because if both a and m are negative, then we have a negative number within the square root and the standard deviation can\'t be imaginary.\r\n\r\nE is eliminated because if m is negative and really large, while a is positive and really small, then the second term dominates the first and we have a positive sum. But F (=ma) is again negative, so sigma_F is again negative, and that is impossible.\r\n\r\nThat leaves C and D. Now we can use another observation: if we can measure either m or a with infinite precision, then its standard deviation would be zero. However because of the other variable, we do not know F with infinite precision, and therefore sigma_F is not zero. Plugging in this condition eliminates D, leaving C as the only possible answer.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
