GREPhysics.NET: GR9277 #42

GR9277 #42

Problem

GREPhysics.NET Official Solution

\prob{42}
A cylinder with moment of inertia 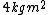$4kgm^2$ about a fixed axis initially rotates at 80 radians per second about this axis. A constant torque is applied to slow it down to 40 radians per second.

If the cylinder takes 10 seconds to reach 40 radians per second, the magnitude of the applied torque is

80 Nm
40 Nm
32 Nm
16 Nm
8 Nm

Mechanics $\Rightarrow$ }Angular Kinematics

Kinematics with angular quantities is exactly like linear kinematics with

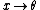$x \rightarrow \theta$ (length to angle)

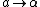$a \rightarrow \alpha$ (linear acceleration to angular acceleration)

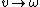$v \rightarrow \omega$ (linear velocity to angular velocity)

$m \rightarrow I$ (mass to moment of inertia)

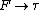$F \rightarrow \tau$ (force to torque).

Thus, one transforms 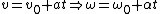$v=v_0+at \Rightarrow \omega=\omega_0+\alpha t$ .

Plugging in the given quantities, one gets 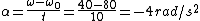$\alpha = \frac{\omega-\omega_0}{t}=\frac{40-80}{10}=-4rad/s^2$ .

The torque is given by 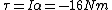$\tau = I \alpha = -16Nm$ , whose magnitude is given by choice (D).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

mvgnzls 2011-09-15 18:23:37	I did this solution: (is it correct)?:: L = IW T= $\dot{L}$ = I $\dot{W}$ = I dW/dt dW = 40 rad/s dt = 10 s I = 4 then T = 16 is this correct? Reply to this comment
crossno 2010-11-12 20:12:16	Just like linear impulse which says: F $\Delta$ t= $\Delta$ P=m $\Delta$ v angular impulse says $\tau$ $\Delta$ t=I $\Delta$ $\omega$ where I=4 $\Delta$ $\omega$ =40 $\Delta$ t=10 therefor $\tau$ =16Nm Reply to this comment
jmason86 2009-09-03 18:52:53	This is similar to grae313's solution.. but here's what went through my head. F=ma T=I $\alpha$ by analogy I = 4 (given) the change in (angular) velocity is 80-40=40 rad/sec Also given that the time it takes to do that change is 10 sec. By units, $\frac{\delta V}{\delta t}$ will give units of rad/s^2 which is an acceleration. So T = 4 * 40/10 = 4*4 = 16 Reply to this comment
grae313 2007-10-14 14:16:38	Here's an alternate solution: $\ N =$ $\frac{dL}{dt} =$ $\frac{\Delta L}{\Delta t} =$ $\frac{I \Delta w}{\Delta t}$ $\ N =$ $\frac{4(40-80)}{10}$ $\ = -16$ The question asks for the magnitude. Reply to this comment

Post A Comment!

You are replying to:

Just like linear impulse which says: F $\Delta$ t= $\Delta$ P=m $\Delta$ v angular impulse says $\tau$ $\Delta$ t=I $\Delta$ $\omega$ where I=4 $\Delta$ $\omega$ =40 $\Delta$ t=10 therefor $\tau$ =16Nm

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone