|
GR9277 #38
|
|
|
Problem
|
|
\prob{38}
Tau leptons are observed to have an average half-life of 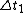 in the frame in the frame 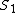 in which the leptons are at rest. In an inertial frame in which the leptons are at rest. In an inertial frame 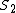 , which is moving at a speed , which is moving at a speed 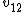 relative to relative to 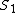 , the leptons are observed to have an average half-life of , the leptons are observed to have an average half-life of 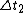 . in another inertial reference frame . in another inertial reference frame 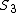 , which is moving at a speed , which is moving at a speed 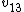 relative to relative to 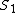 and and 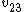 relative to relative to 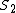 , the leptons have an observed half-life of , the leptons have an observed half-life of 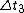 . Which of the following is a correct relationship among two of the half lives, . Which of the following is a correct relationship among two of the half lives, 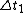 , , 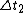 , and , and 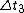 . .
-
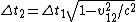
-
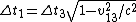
-
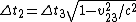
-
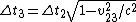
-
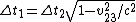
|
Special Relativity }Time Dilation Formula }Time Dilation Formula
The time dilation formula is given by 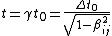 , where time is dilated (lengthened) in all but the frame at rest (proper-time , where time is dilated (lengthened) in all but the frame at rest (proper-time 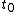 ). Note that ). Note that 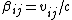 . .
So, from that alone, one can deduce the following relations (without looking at the choices yet):
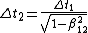
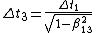
The latter deduction is just choice (B).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
QuantumCat
2014-09-25 08:49:23 | Don't be like me and make the mistake of trying to correlate 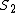 and and 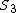 . Since . Since 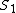 is at rest, it's the only one that can comfortably be dealt with (without addition of velocities or extra terms in the invariant space-time interval). Deal only with the relationship between is at rest, it's the only one that can comfortably be dealt with (without addition of velocities or extra terms in the invariant space-time interval). Deal only with the relationship between 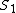 & & 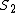 and and 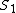 & & 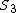 ! ! |  | ender
2009-11-05 23:53:02 | Time interval is shortest in the particle's rest frame. This means 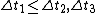 , only choices B and E remain. Choice E involves , only choices B and E remain. Choice E involves 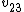 which should not be the case. Hence (B) is the answer. which should not be the case. Hence (B) is the answer. |  | Albert
2009-10-20 13:01:25 | I am not sure whether B is the right answer, despite the unlikelyhood of ETS offering a wrong answer. Or perhaps I have gotten the concept backwards :)
In frame S2 where we are moving with velocity V12 relative to S1, it becomes almost obvious to me that the time T2 should be smaller than T1, given the fact that when I speed up, time around myself speeds up, at least thats what I think because actually my own time (which is the virtual time) has slowed down. Evidently, I would witness the decay process speeding up and the time T2 getting smaller than T1, hence I feel option A should be correct. But since ETS can't be wrong, I suppose I must be!
Albert
2009-11-03 14:44:06 |
And indeed I am! Ignore my comment above, I was high on cocaine when I wrote it! :)
|
tommy22222
2019-10-14 09:14:14 |
Oh Albert, you should be the last person to get this relativity problem wrong even if you were high on coke! :)
|
|  | realcomfy
2008-11-05 15:41:44 | I am confused about the order that the 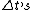 are placed because in the official answer the first deduction corresponds EXACTLY to the answer choice A. Furthermore, the "correct" deduction has are placed because in the official answer the first deduction corresponds EXACTLY to the answer choice A. Furthermore, the "correct" deduction has 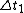 and and 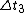 reversed. reversed.
Also, I have on my equation sheet  . Using this convention I was able to get the correct answer. Do I have this backwards, or is there a typo here? . Using this convention I was able to get the correct answer. Do I have this backwards, or is there a typo here?
ramparts
2009-08-09 20:28:31 |
Nope - the Lorentz factor is the reciprocial of 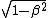 . In the answer, they're multiplying both sides by . In the answer, they're multiplying both sides by 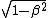 to move it to the other side. to move it to the other side.
|
|  | Poop Loops
2008-10-12 00:19:20 | The reason why C and D don't work is because you don't know whether d-t2 or d-t3 is bigger, and clearly if d-t2 > d-t3 then C doesn't work, and if it's vice versa, D doesn't work. For example if v23 = -v12, that means that S3 is also in the particle's rest frame, and only D works. On the other hand if v23 = v12, then the particle is going much faster in the S3 frame than in the S2 frame, so only C works. Clearly there is a conflict here because you aren't given enough information.
Whereas since S1 is a rest frame, it's stationary and v = 0, therefore if you move to any other frame, v can only go up, so B is the correct relationship between the two for sure.
tommy22222
2019-10-14 09:19:20 |
Even though I picked A which is correct, I wondered for a long time why C and D can\'t be correct. You explained it well!
|
|  | chrisfizzix
2008-10-06 12:42:28 | Minimal notation is a virtue on this silly timed thing:
Take 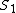 to be the rest frame. Now write time dilation into the other two frames: to be the rest frame. Now write time dilation into the other two frames:
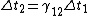
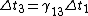
Now notice that all the ugly square root crap that ETS has written is just 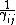 ; from that, we can see that the relations given in the choices are just ; from that, we can see that the relations given in the choices are just
A: 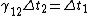
B: 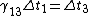
C: 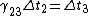
D: 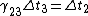
E: 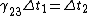
Where B is clearly a correct relation.
GREmania
2008-10-12 08:01:49 |
I like that!
:)
|
apr2010
2010-04-07 18:26:46 |
Good one and I assume this is ETS' intention to confuse the student. Was time dilatation t = t' y or t= t' /y... I like that though, makes me think more about the correctness about what I am reading.
|
|  | callie
2008-04-07 22:16:46 | why couldn't the answer be c, if S2 were assumed to be the rest frame? (if only S2 and S3 were compared against each other) S1 cannot be an "absolute" rest frame, can it?
caffeinated
2008-04-09 14:26:46 |
I, also, am not clear on this since supposedly it doesn't matter who is moving with respect to whom, and is there really any such thing as absolute rest? Not at my desk.
|
rose3fa
2009-08-31 09:23:03 |
S1 can be the absolute rest frame! According to Feynman, in the twin paradox we know the twin that went away and came back is the one whose clock ran slower. Feynman says you cannot imagine that the "traveling" twin stayed still in his own reference frame and the earth moved away from it. Feynman claims that the twin who felt the movement, i.e. accelerated away and decelerated on the way back, is the one whose clock ran slower.
Now, I still have trouble understanding this concept too. But, if we accept Feynman's example, it makes sense to call S1 a rest frame with the fastest clock.
Incidentally, I only quote Feynman's example because I just finished the books, "6 Not So Easy Pieces," which deals with relativity.
|
apps00
2010-10-06 10:08:20 |
It's because when the formula for the time intervals' relation was derived we assumed the particle to have zero velocity in the rest frame.
Let the "2" system move with 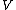 relatively to "1" system, and the particle is in "1" system. The relations between coordinates of two events in these frames are: relatively to "1" system, and the particle is in "1" system. The relations between coordinates of two events in these frames are:
}_1 = \frac{ct^{(1)}_1-\beta x^{(1)}_1}{\sqrt{1-\beta^2}})
}_2 = \frac{ct^{(1)}_1-\beta x^{(1)}_1}{\sqrt{1-\beta^{(2}})
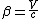
Now we subtract the second equation from the first one to derive relation between two time intervals:
} = \frac{c\Delta t^{(1)}-\beta \Delta x^{(1)}}{\sqrt{1-\beta^2}})
Note, that if the particle is not moving in "1" frame, }) equals to zero and we derive equals to zero and we derive
} = \frac{\Delta t^{(1)}}{\sqrt{1-\beta^2}})
The (C) is not correct because }) is not zero when the lepton doesn't rest in the chosen frame. For this particular case is not zero when the lepton doesn't rest in the chosen frame. For this particular case } = -V_{12}\Delta t_2) and the "correct (C)" relation would be and the "correct (C)" relation would be 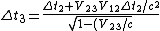^2}}) instead. instead.
|
|  | astro_allison
2005-11-24 21:59:38 | what do we do with the information "in inertial reference frame S3, moving at speed v_23 relative to S2, the observed half-life is 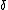 t_3"? t_3"?
astro_allison
2005-11-24 22:00:12 |
...not supposed to be a "partial"t_3, but a "delta"t_3
|
yosun
2005-11-26 01:41:37 |
astro_allison: the extra information for 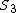 is to confuse the test-taker who does not understand how the time dilation equation works. the time dilation equation relates the time of a rest frame (proper time) to that of a moving frame. None of the choices relate is to confuse the test-taker who does not understand how the time dilation equation works. the time dilation equation relates the time of a rest frame (proper time) to that of a moving frame. None of the choices relate 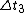 to to 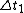
fyi: \Delta produces a capital delta sign 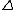 , while \delta produces a lower-case delta sign , while \delta produces a lower-case delta sign 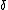 . The lower-case delta . The lower-case delta 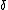 is not the usual sign for a partial derivative (recall that it is used to denote variations in Calculus of Variations). The usual sign for a partial derivative is given by \partial, which produces is not the usual sign for a partial derivative (recall that it is used to denote variations in Calculus of Variations). The usual sign for a partial derivative is given by \partial, which produces  . (Surround the LaTeX command above with dollar signs for them to take effect.) . (Surround the LaTeX command above with dollar signs for them to take effect.)
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
