|
GR9277 #35
|
|
|
Problem
|
|
\prob{35}
Light of wavelength 5200 A is incident normally on a transmission diffraction grating with 2000 lines per cm. The first-order diffraction maximum is at an angle, with respect to the incident beam, that is most nearly
- 3 degrees
- 6 degrees
- 9 degrees
- 12 degrees
- 15 degrees
|
Optics }Diffraction Grating }Diffraction Grating
Diffraction gratings have the same formula as 2-slit interference, except each slit is (obviously) much smaller. The condition for maximum is given by 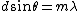 , relating the width of the slit to the wavelength and angle and order m. , relating the width of the slit to the wavelength and angle and order m.
The width of each slit is given by the grating 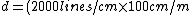^{-1}=0.5E-5 m) . Thus, plugging in the wavelength one has . Thus, plugging in the wavelength one has 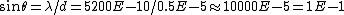 . .
Now, the approximations to get rid of the trig function. Since 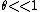 , one can approximate , one can approximate 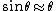 , where the angle is in radians. Now, convert the angle from radians to degrees. , where the angle is in radians. Now, convert the angle from radians to degrees. 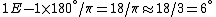 , as in choice (B). , as in choice (B).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
mvgnzls
2011-09-15 15:46:39 | why is d= to the inverse of (number of slits per unit length)?
pam d
2011-09-28 18:15:35 |
If there are 2000 slits per cm, then every slit has to be spaced 1/2000 cm apart. Think about it this way, if you line up 2000 of them in a row (which is what a diffraction grating is) then you'll have a 1 cm long diffraction grating with 2000 slits.
|
Quark
2011-10-26 13:28:09 |
Makes sense, nice Pam!
|
|  | chrisfizzix
2008-10-06 12:24:21 | In the double/N-slit diffraction equation, d is the slit spacing, not the slit width. This problem implicitly assumes that the slits are extremely narrow, so that even though there are 2000 of them in a cm they are much more narrow than they are far apart. Given this interpretation, d = slit spacing = (number of slits in unit length)) = (1 / 2000) cm. The solution is correct besides that. = (1 / 2000) cm. The solution is correct besides that. |  | hungrychemist
2007-09-22 18:58:38 | the diffraction formula, w *sin(angle) = m*wavelength gives minima not the maxima. (See pg 893 Halliday)
to approximate the maxima, one can set m = 1.5 (since the maximum occurs in between the two minima).(See pag 894 Halliday)
following yosun's calculation but with m = 1.5, I found the answer to be nearly 9 degrees.
What's going on?
hamood
2007-10-03 17:40:09 |
The minima is for a single slit diffraction pattern. In this question we have a diffraction grating, and the same formula would give the maxima.
|
alemsalem
2010-09-25 06:06:53 |
grating maxima are at the same angle as interference maxima, this is because the pattern is a multiplication of the interference term and the diffraction term.
but because the slit width is extremely small the first diffraction minima would be at an angle more than 90 degrees which means all the pattern is within the central diffraction maximum and the rest is interference maxima and minima.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
