|
GR9277 #17
|
|
|
|
|
Alternate Solutions |
behnamn90
2013-10-14 17:09:46 | The graph on the oscilloscope is a parametric plot with the parameter being angular frequency ranging from zero to 2pi. This is called a "Lissajous figure" on an oscilloscope used in X-Y mode. The question asks which one is possible? If we have y=-cos(2w) and x=-cos(w) you get (A). If you have y=sin(2w) and x=sin(w) you get (E) rotated 90 degrees so (E) isn't possible. Go on:
http://www.wolframalpha.com/input/?i=parametric+plot+y%3D-cos%282t%29+and+x%3D-cos%28t%29
The correct one is plotted in the link. |  | kstephe6
2012-11-04 18:37:52 | NO MATH HERE!!
This is old skool Electrical Engineer knowledge.
We have a 1:2 frequency ratio. This means the pattern has ONE "hump" in it.
**Extra info below****
(google phase shift chart to get a better idea of what I mean here)
All patterns for the 1:2 ratio look like a 3D wire frame of a Pringle's potato chip or horse saddle rotated about the vertical. (Again, ONE HUMP)
The answer here happens to be the simplest corresponding to a phase shift of 45 degrees which is a side view of the Pringle's potato chip where only the front have is visible and the back half of the chip is eclipsed.
Again, google the chart. You'll see.rnrn |  | nyuko
2009-11-04 07:10:44 | To solve this problem, all I did was to follow the trace and imagine a projection on X and Y. Then you see in (A), Y completes a round trip while X completes half a round trip. So the frequency in Y is twice that of X. Done!
(Sorry, I meant to label this as "user solution" yet didn't know it would be reset after preview) |  | jburkart
2007-11-01 00:20:57 | If we first assume 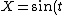) , , 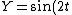) , then we can solve: , then we can solve: 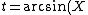) , so , so 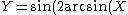)=2\sin(\arcsin(X))\cos(\arcsin(X))) , which then reduces to , which then reduces to 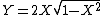 . This is not any of the figures listed, because this problem is extremely unreasonable. However, if we assume instead that . This is not any of the figures listed, because this problem is extremely unreasonable. However, if we assume instead that 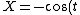) and and 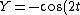) , then it resolves into , then it resolves into 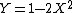 , choice (A). , choice (A). |  | senatez
2006-10-20 09:56:06 | I think it is best to think of it as a vector function which traces out a curve:
f(t) = sin(t)i + sin(2t)j
This can immediately elliminate D and E which would be a vector of the form of an ellipse:
f(t) = cos(t)i + sin(t)j |  | ytsejam
2006-10-17 11:16:56 | The explanation given above is wrong. The oscilloscope is in X-Y mode. So the answer has to be a Lissajous figure. All the options are
Lissajous figures for various frequency ratios.
A) omega_Y = 2* omega_X
B)omega_Y = 4* omega_X
C)omega_Y = 3* omega_X
D)omega_Y = omega_X
E)omega_Y = 1/2 *omega_X |  |
|
|
Comments |
g7d
2014-10-20 18:56:31 | This demonstration should make things clearer. http://demonstrations.wolfram.com/VirtualOscilloscope/ |  | salticus
2014-10-13 11:19:44 | It's a mistake to assume both oscillators are in phase.
What says the oscillators were "switched on" at the same time?
In general, 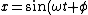) not just not just 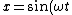) . .
Using 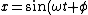, y=sin(2\omega t)) : :
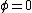 produces an infinity shape, produces an infinity shape,
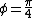 produces a parabola opening upward or a "U" shape, produces a parabola opening upward or a "U" shape,
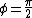 produces that infinity shape again, produces that infinity shape again,
and 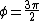 gives a parabola opening downward or a "frown." gives a parabola opening downward or a "frown."
Instead of calculating all that out, I like kstephe6 or nyuko approached it.
kstephe6: imagine the outline of a saddle (i.e. pringles potato chip shape) rotating around the z-axis.
nyuko: check the ratios, and pick the one that fits.
(see their comments for details.) |  | behnamn90
2013-10-14 17:09:46 | The graph on the oscilloscope is a parametric plot with the parameter being angular frequency ranging from zero to 2pi. This is called a "Lissajous figure" on an oscilloscope used in X-Y mode. The question asks which one is possible? If we have y=-cos(2w) and x=-cos(w) you get (A). If you have y=sin(2w) and x=sin(w) you get (E) rotated 90 degrees so (E) isn't possible. Go on:
http://www.wolframalpha.com/input/?i=parametric+plot+y%3D-cos%282t%29+and+x%3D-cos%28t%29
The correct one is plotted in the link. |  | kstephe6
2012-11-04 18:37:52 | NO MATH HERE!!
This is old skool Electrical Engineer knowledge.
We have a 1:2 frequency ratio. This means the pattern has ONE "hump" in it.
**Extra info below****
(google phase shift chart to get a better idea of what I mean here)
All patterns for the 1:2 ratio look like a 3D wire frame of a Pringle's potato chip or horse saddle rotated about the vertical. (Again, ONE HUMP)
The answer here happens to be the simplest corresponding to a phase shift of 45 degrees which is a side view of the Pringle's potato chip where only the front have is visible and the back half of the chip is eclipsed.
Again, google the chart. You'll see.rnrn
kstephe6
2012-11-05 05:06:59 |
In fact, E could be answer IF it were rotated 90 degrees in the plane of the page
|
memyselmineni
2014-11-19 10:17:46 |
I agree! No maths at all. Only frequency ratio is needed! Get help from this book, it nails the physics GRE! http://www.amazon.com/Physics-Mathematica-Jude-Ndubuisi-Onicha/dp/1499691920/ref=sr_1_fkmr1_1?s=books&ie=UTF8&qid=1401627044&sr=1-1-fkmr1&keywords=physics+mathematica++2nd+edition+by+onicha+jude
|
|  | alanalan
2012-09-11 16:11:22 | Something is terribly wrong here! If answer E is correct when X is twice the frequency of Y, then it should be the same but rotated by 90 degrees when Y is twice the frequency of X. You are just swapping the axis when the frequencies are swapped.
That means none of the answers are correct! |  | niux
2009-11-06 10:39:39 | ETS were nonsense in this answer. The condition that spot is initially at the center of the screen: IT IS THIS INITIAL CONDITION, that inmediatly discard (A), (B) and (D). NO MATTER WHAT THE RATIO OF FREQUENCY IS.
Then answer should be (E)
niux
2009-11-06 10:45:36 |
My last line is wrong, answer shuould not be (E) beacuse ratio of frequency is 1:2 (y:x) and not (2:1).
Anyway, as neither (C) satisfies this condition.
I Repeat: ETS were non sense in this one
|
neon37
2010-11-10 11:36:45 |
have you never used an oscilloscope? It refreshes everyone once in a while depending on what you set. The cursor being at the center means that the oscilloscope is calibrated or rather adjusted in such a way. This shapes that appear are the oscillations about the center and not spatially shifted.
|
|  | nyuko
2009-11-04 07:10:44 | To solve this problem, all I did was to follow the trace and imagine a projection on X and Y. Then you see in (A), Y completes a round trip while X completes half a round trip. So the frequency in Y is twice that of X. Done!
(Sorry, I meant to label this as "user solution" yet didn't know it would be reset after preview) |  | nyuko
2009-11-04 07:09:36 | To solve this problem, all I did was to follow the trace and imagine a projection on X and Y. Then you see in (A), Y completes a round trip while X completes half a round trip. So the frequency in Y is twice that of X. Done! |  | nyuko
2009-10-30 09:50:21 | I never remember a single expression for this kind of problem. I even didn't know the trace has a fancy name.
To solve this problem, all I did was to follow the trace and imagine a projection on X and Y. Then you see in (A), Y completes a round trip while X completes half a round trip. So the frequency in Y is twice that of X. Done!
|  | chrisfizzix
2008-10-06 11:19:20 | This is a totally dick question.
Just to be constructive about it and all.
GREmania
2008-10-12 06:08:07 |
yeah, it is. Haha
|
|  | jburkart
2007-11-01 00:20:57 | If we first assume 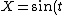) , , 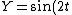) , then we can solve: , then we can solve: 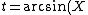) , so , so 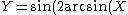)=2\sin(\arcsin(X))\cos(\arcsin(X))) , which then reduces to , which then reduces to 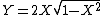 . This is not any of the figures listed, because this problem is extremely unreasonable. However, if we assume instead that . This is not any of the figures listed, because this problem is extremely unreasonable. However, if we assume instead that 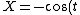) and and 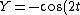) , then it resolves into , then it resolves into 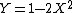 , choice (A). , choice (A). |  | jburkart
2007-11-01 00:20:39 | If we first assume 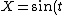) , , 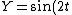) , then we can solve: , then we can solve: 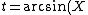) , so , so 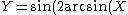)=2\sin(\arcsin(X))\cos(\arcsin(X))) , which then reduces to , which then reduces to 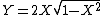 . This is not any of the figures listed, because this problem is extremely unreasonable. However, if we assume instead that . This is not any of the figures listed, because this problem is extremely unreasonable. However, if we assume instead that 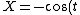) and and 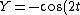) , then it resolves into , then it resolves into 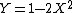 , choice (A). , choice (A). |  | dcb
2007-09-16 14:51:46 | While I initially thought it was E (a Lissajous curve), writing a simple example sheds some light.
Lets take a time interval from 0 to 8 (the scale is arbitrary for an easy integer example).
- In this interval, X will go from 0 to 4 and back to 0 (one oscillation).
- Y, with twice the frequency, will go from 0 to 4 to 0 to 4 to 0.
Simply, (using a linear example):
T X Y
0 0 0
1 1 2
2 2 4
3 3 2
4 4 0 <--(at this point, X has gone through half a period,
5 3 2 Y has gone through a full period)
6 2 4
7 1 2
8 0 0
Plot X vs Y, It a simple triangular looking hump, similar to A. It is linear because I made the input waves linear for simplicity. However, it does not have to be.
danksci
2008-09-08 14:29:09 |
According to the question shouldnt 0 strart at the center of the screen?
|
taatliberty
2011-10-11 14:54:51 |
Yeah. Plus, Y should go negative as it continues through the oscillation.
|
|  | kwooley
2007-04-06 19:08:43 | Here is a link to a nice aplet that should help answer questions about this problem
http://ibiblio.org/e-notes/Lis/Lissa.htm |  | hamood
2007-04-01 16:23:46 | The way I went about this was by just doing a rough plot
y = 1,0,-1,0,1,0,-1,0,1 (period 0f 4)
x=4,3,2,1,0,1,2,3,4 (period of 8)
The plotted graph looks likes A.... |  | SonOfOle
2006-11-02 21:27:32 | x123. Check the link you supplied again. They give a Lissajous curve that looks exactly like (A) on that page where the ratio of the frequencies is 1:2. |  | senatez
2006-10-20 09:56:06 | I think it is best to think of it as a vector function which traces out a curve:
f(t) = sin(t)i + sin(2t)j
This can immediately elliminate D and E which would be a vector of the form of an ellipse:
f(t) = cos(t)i + sin(t)j |  | senatez
2006-10-20 09:52:29 | |  | ytsejam
2006-10-17 11:16:56 | The explanation given above is wrong. The oscilloscope is in X-Y mode. So the answer has to be a Lissajous figure. All the options are
Lissajous figures for various frequency ratios.
A) omega_Y = 2* omega_X
B)omega_Y = 4* omega_X
C)omega_Y = 3* omega_X
D)omega_Y = omega_X
E)omega_Y = 1/2 *omega_X
D8less
2007-10-02 17:30:06 |
Thank you, I was waiting for someone to say this.
|
Poop Loops
2008-10-05 13:41:47 |
This is by far the easiest way to look at it.
|
kroner
2009-11-04 23:35:31 |
To be a nitpicky, (B) is actually just a nonsensical image. Notice at both extremes of X, Y seems to turn around at zero rather than reaching -1.
|
crossno
2010-11-12 18:03:01 |
I agree, this is the correct way to do it. except both B and C are omega_y=3*omega_x.....the only difference is the phase
the answer is A
|
|  | x123
2006-10-17 08:56:46 | I think the answer is (E), because it's a Lissajous curve.
http://en.wikipedia.org/wiki/Lissajous_curve
europa
2006-11-01 22:11:01 |
ETS says it is A but only 10 percent scored this answer correctly so go figure...
|
ducksquark
2007-11-02 05:28:41 |
It should be a Lissajous figure all right. But (E) shows the figure for the wrong freq. ratio. (X being twice the freq of Y -- see wikipedia article -- the example figure given there is (E) turned on is side.)
|
taatliberty
2011-10-11 15:01:25 |
Europe, where did you get the answer list?
|
|  |
|
| Post A Comment! |
You are replying to:
While I initially thought it was E (a Lissajous curve), writing a simple example sheds some light.
Lets take a time interval from 0 to 8 (the scale is arbitrary for an easy integer example).
- In this interval, X will go from 0 to 4 and back to 0 (one oscillation).
- Y, with twice the frequency, will go from 0 to 4 to 0 to 4 to 0.
Simply, (using a linear example):
T X Y
0 0 0
1 1 2
2 2 4
3 3 2
4 4 0 <--(at this point, X has gone through half a period,
5 3 2 Y has gone through a full period)
6 2 4
7 1 2
8 0 0
Plot X vs Y, It a simple triangular looking hump, similar to A. It is linear because I made the input waves linear for simplicity. However, it does not have to be.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
