GREPhysics.NET: GR8677 #64

GR8677 #64

Problem

GREPhysics.NET Official Solution

Electromagnetism $\Rightarrow$ }Impedance Matching

Because the capacitor is fully charged, it is the generator. The inductor, which opposes the current as the capacitor discharges, is the load. Impedance matching requires that the impedance of the generator and load are the same. However, since $Z_g=R_g+jX_g$ and $Z_L = R_l + j X_l$ , for the generator and load, respectively, and $X_g = X_{gL} - X_{gC} = -X{gC}$ and $X_l = X_{lL} - X_{lC} = X_{IL}$ , one finds that for impedance matching, $X_g = -X_l$ .

More info here

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

physics_guy
2018-08-08 21:13:34

There are two kinds of impedance matching. One minimizes reflection at the boundary between materials, and the other maximizes power transfer between two materials. To minimize reflection, the impedance of the generator must equal the impedance of the load. To maximize power transfer, the impedance of the generator must equal the complex conjugate of the impedance of the load. If we wanted to minimize reflection, (B) would be the correct answer. Since we instead want to maximize power transfer, (C) is the correct answer.

Reply to this comment

Marian
2016-01-05 08:57:59

http://http://grephysics.net

Reply to this comment

Marian
2016-01-05 08:56:56

Neige Hunter: montres, nerds pourrait knock réplique Breitling Bentley Flying B plongée en apnée, il est prêt, durée du rythme cardiaque, mais tout le monde peut être dit de se concentrer sur la conception, \"et alors, regardez cette heure génial !.\"\r\n\r\nreplique " target="_blank">http://www.repliquemontresfr.eu\">replique montre

Reply to this comment

Marian
2016-01-05 08:56:09

http://www.repliquemontresfr.eu

Reply to this comment

nishamgu
2011-12-19 22:56:11

prove the commutation relation[L_k,r^2]=0 where r is the radius vector

Reply to this comment

jw111
2008-09-01 15:11:23

You need to know two things
(1) The impedance is the resistance of object in AC circuit.
(2) The imaginary part of impedance control the PHASE of voltage(cross the object) and current (through the object).

In this problem, we can treat the circuit as an IDEA POWER SOURCE + an OBJECT with impedance equal to

$R_g+R_g+jX_g+jX_l$

with the max power transfer to the OBJECT
the phase of V and I must be inphase that the imaginary part of effective impedance must be 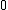$0$ .

Thus 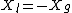$X_l=-X_g$

Reply to this comment

RebeccaJK42
2007-03-15 14:22:16

Why is it negative Xg and not positive Xg?

Blake7
2007-09-21 19:18:17

One needs the 'imaginary' reactances to cancel out and thus 'match the impedance'

Reply to this comment

sharpstones
2006-10-19 13:49:09

What's this about a capacitor and an inductor? Problem 64 from 86 exams says "An alternating current electrical generator has a fixed internal impedance..." ?

Reply to this comment

yosun
2005-12-06 20:24:53

jax: thanks for the correction.

Reply to this comment

jax
2005-12-02 21:27:25

This one confused me at first so let me clarify,

To maximize the power transfer, the impedance needs to be 'matched'. The impedance is 'matched' if the load impedance equals the complex conjugate of the source impedance, 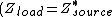$(Z_{load} = Z_{source}^*)$ .

In our case 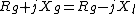$R_g + jX_g = R_g - jX_l$ maximizes the power transfer, so $X_l = - X_g$ .

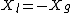jax
2005-12-02 21:28:16

Lots more info here: http://en.wikipedia.org/wiki/Impedance_matching#Complex_conjugate_matching

RusFortunat
2015-10-21 14:21:02

Now it is clear. Thank you

Reply to this comment

Post A Comment!

You are replying to:

jax: thanks for the correction.

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone