|
GR8677 #29
|
|
|
|
|
Alternate Solutions |
mahdisadjadi
2012-09-27 10:06:49 | The answer is definitely B. As you can see, test charge is negative and the official solution points it out. But in the answer this is not considered.
Assume that:
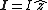
In this situation, direction of magnetic field is in the right hand side along 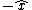 and is along and is along 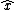 in the left hand side of wire, so we can write , by Loentz force law(we take q to be positive and enter a minus to indicate negativity of charge): in the left hand side of wire, so we can write , by Loentz force law(we take q to be positive and enter a minus to indicate negativity of charge):
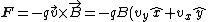)
Force should be parallel to the current, so we take 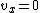 and and 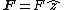 , where , where 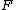 should be positive. should be positive.
So, 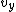 is negative and charge is moving away from the wire. is negative and charge is moving away from the wire.
|  |
|
|
Comments |
fredluis
2019-08-09 04:35:04 | They do not specify a theta dependence for the wave function so you can assume it is only a function of phi. Normalize the given function. irrigation repair |  | joshuaprice153
2019-08-09 02:44:23 | I can not thank you sufficiently for the articles on your web-site. I know you place a lot of time and energy into these and hope you know how considerably I enjoy it. I hope I\'ll do the identical thing man or woman at some time. 100% commission Gainesville |  | kronotsky
2018-10-23 03:44:30 | Right hand rule trick: if you put your thumb in the direction of I, and curl your fingers up into a fist, the fingers point along B. We want 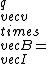 . Cyclic permutations and setting . Cyclic permutations and setting 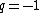 gives gives 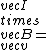 . . |  | QuantumCat
2014-09-02 14:01:17 | Consider 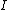 = = 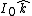 so that so that 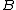 = = 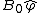 . Because q goes to -q, consider that . Because q goes to -q, consider that 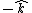 = = 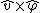 so so ) leading to choice A leading to choice A |  | mahdisadjadi
2012-09-27 10:06:49 | The answer is definitely B. As you can see, test charge is negative and the official solution points it out. But in the answer this is not considered.
Assume that:
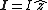
In this situation, direction of magnetic field is in the right hand side along 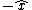 and is along and is along 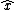 in the left hand side of wire, so we can write , by Loentz force law(we take q to be positive and enter a minus to indicate negativity of charge): in the left hand side of wire, so we can write , by Loentz force law(we take q to be positive and enter a minus to indicate negativity of charge):
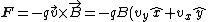)
Force should be parallel to the current, so we take 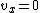 and and 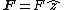 , where , where 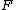 should be positive. should be positive.
So, 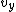 is negative and charge is moving away from the wire. is negative and charge is moving away from the wire.
walczyk
2012-10-13 13:06:27 |
Uh if Vy is negative then it is moving TOWARD the wire, not away from it. Also the answer is A, if ETS gave the wrong answer you wouldn't be the only one discovering this. This test is very very old.
|
eris1
2015-10-08 14:48:11 |
Define the cable as laying on the  -axis at the origin of the -axis at the origin of the 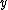 and and  axis. Imagine the particle is moving strictly along the y axis, starting at a point axis. Imagine the particle is moving strictly along the y axis, starting at a point 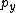 >0. With a negative velocity (in the negative >0. With a negative velocity (in the negative 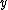 direction), the particle is moving towards the wire and the direction), the particle is moving towards the wire and the 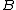 -field it encounters is in the positive -field it encounters is in the positive  -direction. If the particle starts at -direction. If the particle starts at 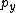 <0 then the direction of the <0 then the direction of the 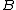 -field it encounters is in the negative -field it encounters is in the negative  direction (canceling the \"-\" from the charge), thus following that the velocity of the particle must be positive (for a positive force), moving again towards the wire. direction (canceling the \"-\" from the charge), thus following that the velocity of the particle must be positive (for a positive force), moving again towards the wire.
|
camarasi
2017-10-25 14:05:56 |
The x-component of the B-field as you\'ve taken it is negative, so you\'re off by a sign.
|
|  | Fily
2011-04-07 04:12:37 | This is more simple just z=-?*Phi(The angle).So its ultimately give ?=-r |  | shafatmubin
2009-10-31 18:12:46 | Fleming's left-hand rule (thuMb for motion, First for field, seCond for current) is used to find direction of motion (i.e. force applied) when current and field directions are known.
So the LHR will work here, if one takes into account of the direction of the CURRENT produced by negative charges (i.e. opposite to velocity direction). |  | dean
2008-10-09 21:45:23 | I may be mistaken, but it seems to me the LHR yields the wrong answer here if used consistently (i.e. twice). Better to stick with the right hand (sorry southpaws) and remember sign.
neon37
2008-11-02 15:41:09 |
not really you are probably trying to figure out the direction of the magnetic field also with LHR. The direction of the field is always with the RHR. You could find the direction the test charge should go given the direction of the field and current, with LHR. I would also suggest sticking to RHR on the real exam. Might be confusing.
|
|  | darox
2006-11-29 06:59:15 | actually, it cannot be B. the direction of the particle would be not parallel, but anti-parallel.
zaharakis
2007-01-05 09:31:42 |
Anti Parallel is still parallel
|
madfish
2007-11-02 12:11:27 |
not when you're talking about relative to a current
|
FortranMan
2008-10-19 13:14:30 |
I thought anti-parallel is still parallel too, until I looked at options (A) and (B).
This problem is deceptively simple, people. Remember that if the charge is moving towards the wire its velocity vector would be negative, but this negative can be canceled out if you are using a negative test charge, resulting in the positive force direction parallel to the positive current direction. In short, the sign of the charge can affect the vector.
|
|  | zaharakis
2006-11-02 14:25:53 | The answer could also be B. The question states parallel to the direction of the current. B would produce a force in the opposite direction to the current but this is still parallel.
zaharakis
2007-01-05 09:31:14 |
Anti parallel is still parallel.
|
tau1777
2008-10-31 19:30:03 |
yeah, i did not realize this the first time i took the test. and as i was redoing it today it hit me, this confusing thing about parallel. i feel that they should be more direct but i guess that's just the ETS. i'll have to keep an eye on my common sense of things and try to see it their way, least until test day. bottom line: to the ETS antiparallel and parallel are different.
|
gt2009
2009-06-22 06:04:21 |
Anti-parallel and parallel are different.
|
|  |
|
| Post A Comment! |
You are replying to:
The answer is definitely B. As you can see, test charge is negative and the official solution points it out. But in the answer this is not considered.
Assume that:
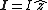
In this situation, direction of magnetic field is in the right hand side along 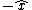 and is along 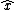 in the left hand side of wire, so we can write , by Loentz force law(we take q to be positive and enter a minus to indicate negativity of charge):
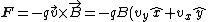)
Force should be parallel to the current, so we take 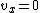 and 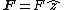 , where 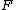 should be positive.
So, 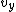 is negative and charge is moving away from the wire.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
