|
GR8677 #28
|
|
|
|
|
Alternate Solutions |
Giubenez
2014-10-22 02:42:06 | The only way to solve this problem is to remember the first Spherical Harmonics, or, at least, their dependence to 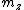 . .
In fact, using the conventional coordinates where ![\theta \in [0,\pi]](/cgi-bin/mimetex.cgi?\theta \in [0,\pi]) is the polar angle and is the polar angle and ![\phi\in [0,2\pi]](/cgi-bin/mimetex.cgi?\phi\in [0,2\pi]) is the azimutal angle, they always have a term is the azimutal angle, they always have a term
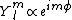 . .
The direction is to estimate A, we have thus to integrate on 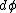 that in the question is CAPITALIZED and we have to choose the that in the question is CAPITALIZED and we have to choose the ![[0,2\pi]](/cgi-bin/mimetex.cgi?[0,2\pi]) interval interval |  |
|
|
Comments |
fredluis
2019-08-09 04:33:09 | This problem is deceptively simple, people. Remember that if the charge is moving towards the wire its velocity vector would be negative. tree removal |  | joshuaprice153
2019-08-09 02:42:01 | I had found that the information is very helpful. That’s a awesome article you posted.I will come back to read some more. towing service |  | Giubenez
2014-10-22 02:42:06 | The only way to solve this problem is to remember the first Spherical Harmonics, or, at least, their dependence to 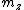 . .
In fact, using the conventional coordinates where ![\theta \in [0,\pi]](/cgi-bin/mimetex.cgi?\theta \in [0,\pi]) is the polar angle and is the polar angle and ![\phi\in [0,2\pi]](/cgi-bin/mimetex.cgi?\phi\in [0,2\pi]) is the azimutal angle, they always have a term is the azimutal angle, they always have a term
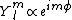 . .
The direction is to estimate A, we have thus to integrate on 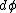 that in the question is CAPITALIZED and we have to choose the that in the question is CAPITALIZED and we have to choose the ![[0,2\pi]](/cgi-bin/mimetex.cgi?[0,2\pi]) interval interval |  | alemsalem
2009-09-23 19:47:52 | i think the answer is correct but the it's missing smthing,, how do u know u should integrate over 2 PI u should integrate over one PI and the other half is accounted for by symmetry there are no additional probabilities,, that would compensate for the factor of 2 pauli mentioned
flyboy621
2010-11-14 19:33:17 |
The integration is over all possible values of 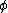 . Since the given function is periodic, you only need to integrate over the period, which is . Since the given function is periodic, you only need to integrate over the period, which is 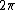 . .
|
|  | pauli568
2007-10-12 13:48:01 | I think there is no correct answer given here.
The con dition of normalization goes as
\int{psi}dv=1 in which case theta coordinate should aso be taken care of and wich will result in an extra 2.
The result should be \frac{1}{2\sqrt{pi}}
dean
2008-10-09 21:40:08 |
The official solution is essentially correct, though I think it's better to think of the normalization as <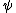 | |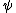 >=1, you get the conjugation for free. >=1, you get the conjugation for free.
|
HaveSpaceSuit
2008-10-17 17:50:12 |
They do not specify a theta dependence for the wave function so you can assume it is only a function of phi. Normalize the given function.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
