|
GR0177 #95
|
|
|
|
|
Alternate Solutions |
RusFortunat
2015-10-16 22:17:54 | What if we simply use the fact that 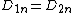 on the border, or on the border, or 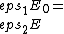 . Applying this to our conditions we get . Applying this to our conditions we get 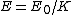 . . |  | fcarter
2008-10-13 17:16:57 | Another one where limits are the fast way. For K->1, E->E. For K->inf, E->0. Only answer that satisfies is A. |  | Mexicana
2007-10-02 17:57:24 | Another way to increase your chances of getting it right is by elimination of choices B, C and D since using dimensional analysis only choice A and E have the correct dimensions of electric field ( 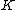 is dimensionless). If with this you also remember the fact that a dielectric under an applied electric field, induces an internal field so that the total field inside decreases, then only choice A remains (as this is the only one which would decrease the original field is dimensionless). If with this you also remember the fact that a dielectric under an applied electric field, induces an internal field so that the total field inside decreases, then only choice A remains (as this is the only one which would decrease the original field 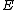 ). ). |  | herrphysik
2006-10-02 18:42:02 | Just use the equation (4.35 in Griffiths) 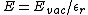 where where 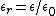 is the relative permittivity. Plug in the given is the relative permittivity. Plug in the given 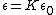 to get the correct answer. to get the correct answer. |  |
|
|
Comments |
RusFortunat
2015-10-16 22:17:54 | What if we simply use the fact that 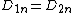 on the border, or on the border, or 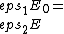 . Applying this to our conditions we get . Applying this to our conditions we get 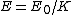 . .
RusFortunat
2015-10-16 22:20:53 |
D: in preview it was more nice
|
|  | johnVay
2013-10-16 19:06:28 | dielectics (like in capacitors) increasing rearranging their internal charges to oppose
the E field. in the limit they are conductors where they rearrange perfectly.
the order:
vacuum - dielectic - conductor
dielectrics always scaling the electric field by kappa. this leaves a and b, you need a little more to recognize that B has an extra factor of epsilon |  | fcarter
2008-10-13 17:16:57 | Another one where limits are the fast way. For K->1, E->E. For K->inf, E->0. Only answer that satisfies is A.
f4hy
2009-11-07 00:27:13 |
Doesn't (B) satisfy those limits as well?
|
|  | Mexicana
2007-10-02 17:57:24 | Another way to increase your chances of getting it right is by elimination of choices B, C and D since using dimensional analysis only choice A and E have the correct dimensions of electric field ( 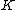 is dimensionless). If with this you also remember the fact that a dielectric under an applied electric field, induces an internal field so that the total field inside decreases, then only choice A remains (as this is the only one which would decrease the original field is dimensionless). If with this you also remember the fact that a dielectric under an applied electric field, induces an internal field so that the total field inside decreases, then only choice A remains (as this is the only one which would decrease the original field 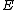 ). ).
Moush
2010-09-18 15:55:06 |
Choice C has the same units as A and E so you can't eliminate it based only on dimensional analysis, but it's intuitive that 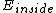 < < 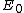 . .
|
|  | Mexicana
2007-10-02 17:52:53 | Another way to increase your chances of getting it right is by elimination of choices B, C and D since using dimensional analysis only choice A and E have the correct dimensions of electric field (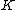 is dimensionless). is dimensionless). |  | herrphysik
2006-10-02 18:42:02 | Just use the equation (4.35 in Griffiths) 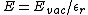 where where 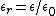 is the relative permittivity. Plug in the given is the relative permittivity. Plug in the given 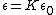 to get the correct answer. to get the correct answer. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
