|
GR0177 #85
|
|
|
|
|
Alternate Solutions |
BerkeleyEric
2010-10-03 11:38:34 | Since the resistance is directly proportional to the length and inversely proportional to the area, we know that the longer wire is four times as resistant as the shorter one. This means that the voltage drop is four times as much for the longer wire, so it is ) . Subtracting this from 8.0 V gives the answer, (A). . Subtracting this from 8.0 V gives the answer, (A). |  | BerkeleyEric
2010-10-03 11:38:02 | Since the resistance is directly proportional to the length and inversely proportional to the area, we know that the longer wire is four times as resistant as the shorter one. This means that the voltage drop is four times as much for the longer wire, so it is ) . Subtracting this from 8.0 V gives the answer, (A). . Subtracting this from 8.0 V gives the answer, (A). |  | 94709
2007-10-29 23:04:05 | You can calculate current although one doesn't have to. This is just a voltage divider.
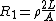 , , 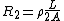 , , 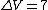 Volts. Volts.
Therefore,
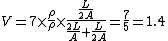
Since the base is 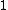 V, the potential at the dividing segment is 2.4V. V, the potential at the dividing segment is 2.4V. |  |
|
|
Comments |
Dudeleb
2016-10-27 15:16:34 | here is a fun little rhyme to help you remember the resistance of a wire. Resistance = RHO RHO RHO YOUR BOAT L OVER A! RESISTANCE RESISTANCE RESISTANCE LIFE IS BUT A DREAM (of an electron traveling down some conducting material). The rest is math. Plug and chug. Like a beer. Am I RIGHT!? Ah man. This test is making me crazy. Cheers all. |  | ChildAtPlay
2012-04-16 04:14:14 | R = rho * L / A. Rho is the same for both wires.
Setting L = 1, A = 1:
Wire 1: R1 = 2L/A = 2
Wire 2: R2 = L/2A = 1/2
Rtotal = R1 + R2 = 2.5.
deltaV for wire 2 is R2/Rtotal = 0.5/2.5 = 0.2.
The voltage drop across wire 2 is 20% of the total voltage drop (Kirchoff).
Voltage @ junction = 1V + 0.2 * (8V-7V) = 1V + 1.4V = 2.4V.
|  | BerkeleyEric
2010-10-03 11:38:34 | Since the resistance is directly proportional to the length and inversely proportional to the area, we know that the longer wire is four times as resistant as the shorter one. This means that the voltage drop is four times as much for the longer wire, so it is ) . Subtracting this from 8.0 V gives the answer, (A). . Subtracting this from 8.0 V gives the answer, (A). |  | BerkeleyEric
2010-10-03 11:38:02 | Since the resistance is directly proportional to the length and inversely proportional to the area, we know that the longer wire is four times as resistant as the shorter one. This means that the voltage drop is four times as much for the longer wire, so it is ) . Subtracting this from 8.0 V gives the answer, (A). . Subtracting this from 8.0 V gives the answer, (A). |  | grae313
2007-11-01 10:17:36 | Alternately, (and this is essentially equivalent 94709's solution, but involves simpler calculations, IMO), once you have the two resistances for the two wires, you can realize that 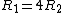 which means that the ratio of the voltage drops in each wire segment has to be 1:4, or: which means that the ratio of the voltage drops in each wire segment has to be 1:4, or:
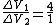 and also and also
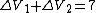
easy math to arrive at the answer.
grae313
2007-11-01 10:17:59 |
ack, I meant to classify this as an alternate solution
|
|  | 94709
2007-10-29 23:04:05 | You can calculate current although one doesn't have to. This is just a voltage divider.
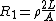 , , 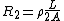 , , 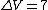 Volts. Volts.
Therefore,
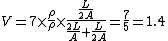
Since the base is 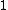 V, the potential at the dividing segment is 2.4V. V, the potential at the dividing segment is 2.4V.
94709
2007-10-29 23:14:15 |
eh, you might not be checking this site any more, but thanks a lot, yosun.
|
|  | keflavich
2005-11-10 22:38:30 | There are a few typos here. 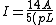}) , you left out the 5. That 0 at the end should be a ')'. , you left out the 5. That 0 at the end should be a ')'.
But also... where does the 1 come from in 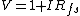 ? ?
yosun
2005-11-10 22:49:04 |
keflavich: thanks for the typo alert; the typo has been corrected.
the 1 comes from the fact that the potential at the end of the fatter wire is 1V, and thus the voltage across the junction is just the voltage at the end of the fat wire plus the current times the resistance of the fatter wire. (i tend to leave off the units to avoid confusion with variables)
|
Richard
2007-10-29 10:07:52 |
A perhaps conceptually easier approach would be to simply find the potential difference across the first wire, and then subtract it from the potential at the end of the thin wire. In my view, this is consistent with how you went about finding the current...
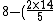=2.4)
|
jmason86
2009-07-09 23:54:25 |
Alternatively, you could have done 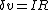  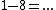 yielding the same value for I, but negative. yielding the same value for I, but negative.
Then following along Yosun's line (where he implied 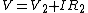 ), we now have instead, ), we now have instead, 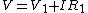 where I is now negative. Plug in to get where I is now negative. Plug in to get 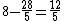
I was kind of confused by the above response that Yosun gave using the fatter wire for everything... so I decided to try flipping it around to make sure it still works... and it does :)
Cheers
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
