|
GR0177 #6
|
|
|
|
|
Alternate Solutions |
physgre
2015-10-15 02:19:22 | 参考卡诺循环图 |  | buaasyh
2014-10-17 02:29:43 | In the adiabatic case, the gas lose tempreture because work has been done by the gas. In the isothermal case, the gas maintains tempreture so the presure is higher than the adiabatic case. Therefore, the work done in the isothermal case is more, i.e., $W_i>W_a$. |  | ProofbyInspection
2010-11-12 09:05:34 | You just need to notice that for ideal gases, isothermic expansion follows a PV curve rnrn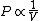 rnrnwhile adiabatic expansion follows a PV curve rnrn rnrnwhile adiabatic expansion follows a PV curve rnrn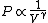 rnrnGiven that these curves start at the same point, because $\gamma>1$ it is pretty clear that the isothermic expansion curve will always be greater than the adiabatic PV curve, and hence does more work. The answer must be (E). rnrnGiven that these curves start at the same point, because $\gamma>1$ it is pretty clear that the isothermic expansion curve will always be greater than the adiabatic PV curve, and hence does more work. The answer must be (E). |  | tau1777
2008-10-23 21:00:29 | So my thermo teacher told us a neat trick that helps make this quicker. so if you realize that an adiabat connects to isotherms on the p-v diagrams. you can convince yourself that the isotherm covers more area. this is because the adiadat has to be steeper in order to connect the two isotherms, and therefore cover less areas. of course i keep mentioning area because work is the area of a curve on a p-v diagram. hope this helps. |  |
|
|
Comments |
yummyhat
2017-10-25 03:54:03 | very similar to question #29 on the 2017 practice exam. |  | physgre
2015-10-15 02:19:22 | 参考卡诺循环图 |  | buaasyh
2014-10-17 02:29:43 | In the adiabatic case, the gas lose tempreture because work has been done by the gas. In the isothermal case, the gas maintains tempreture so the presure is higher than the adiabatic case. Therefore, the work done in the isothermal case is more, i.e., $W_i>W_a$. |  | ProofbyInspection
2010-11-12 09:05:34 | You just need to notice that for ideal gases, isothermic expansion follows a PV curve rnrn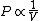 rnrnwhile adiabatic expansion follows a PV curve rnrn rnrnwhile adiabatic expansion follows a PV curve rnrn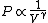 rnrnGiven that these curves start at the same point, because $\gamma>1$ it is pretty clear that the isothermic expansion curve will always be greater than the adiabatic PV curve, and hence does more work. The answer must be (E). rnrnGiven that these curves start at the same point, because $\gamma>1$ it is pretty clear that the isothermic expansion curve will always be greater than the adiabatic PV curve, and hence does more work. The answer must be (E). |  | meitnerium
2010-10-10 21:08:55 | When you wrote
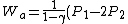 V_1)
how did you flip the sign from the original formula for work done by an adiabatic process, which is:
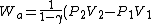 )
|  | gryphia
2008-11-02 14:55:30 | Unless I'm not totally mistaken, this problem can be thought of in the following way:
Work done by an ideal gas is just PdV. For an isotherm, the pressure decreases with 1/V (this comes right from the ideal gas equation, PV=NkT, so P=NkT/V, N and T are constant). For an adiabat, the pressure decreases with 1/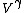 . Now, . Now, 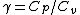 and is greater than 1 for an ideal gas. So the pressure decreases more for the same volume change for an adiabat vs. an isotherm, thus the work done must be less for the adiabat. and is greater than 1 for an ideal gas. So the pressure decreases more for the same volume change for an adiabat vs. an isotherm, thus the work done must be less for the adiabat.
This is equivalent to the work under the curve formulations people have offered above, but may help you if you can't remember the shape of the curves off the top of your head. |  | tau1777
2008-10-23 21:00:29 | So my thermo teacher told us a neat trick that helps make this quicker. so if you realize that an adiabat connects to isotherms on the p-v diagrams. you can convince yourself that the isotherm covers more area. this is because the adiadat has to be steeper in order to connect the two isotherms, and therefore cover less areas. of course i keep mentioning area because work is the area of a curve on a p-v diagram. hope this helps.
NervousWreck
2017-03-28 09:12:16 |
This is a very good solution and I used it too.
|
|  | realcomfy
2008-10-19 04:12:34 | How did you derive the equation for adiabatic work? I am getting lost on this step because I am not sure how the integration would work since we have both varying pressure and volume. Thanks |  | QEDisGoodForMe
2008-10-12 19:54:46 | Just want to say thank you to all who contribute to this website!! You are all amazing, especially Yosun! |  | KarstenChu
2007-03-22 12:55:40 | I think you meant to type P1V1=P2V2 for your derivation of the work done by an isothermal process. |  | tdixon2
2006-09-12 03:26:40 | Easier solution is to realise that the pressure is higher during the isothermal process since energy is added to the gas to keep a constant temperature. Thus dW=PdV is greater for the isothermal process as P is larger at every step and you don't even need to do any math ... hey presto. |  | daschaich
2005-11-10 21:53:01 | The all-important links:
http://en.wikipedia.org/wiki/Image:Adiabatic.png />
http://en.wikipedia.org/wiki/Isothermal_process />
http://en.wikipedia.org/wiki/Adiabatic_process
Walter
2008-08-10 16:38:49 |
I agree with this poster - the graphs tell you everything you need to know.
In a quasi-static process, (and this condition is in the question), the adiabats are always steeper than the isotherms
The work done is the area under these curves so from a given starting point the work done by the isothermal expansion must be greater. You'd have a lot of fun following the mathematical approach in the time available, though it's good to see it!
|
|  | keflavich
2005-11-10 11:03:39 | How do you get from the equations for Wa and Wi to choice E? I had difficulty doing that without a calculator, since 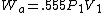 and and 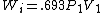 . Are there any good approximations to use? Without the knowledge that adiabatic processes do less work than isothermal, I don\'t think there\'s a reasonable way to come to that answer. . Are there any good approximations to use? Without the knowledge that adiabatic processes do less work than isothermal, I don\'t think there\'s a reasonable way to come to that answer.
daschaich
2005-11-10 21:47:43 |
The way I did it was to remember the PV (pressure vs. volume) diagrams for adiabatic and isothermal processes. I figure somebody's going to remember anything from introductory thermal physics, it's PV diagrams.
I recalled that the PV curves for adiabatic processes are steeper than those for isothermal processes. Since the work done by the gas is the area under the gas is the area under the curve (i.e., 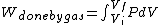 ), we know that the magnitude of the work done by the isothermal process is greater than the magnitude of that done by the adiabatic process. Since ), we know that the magnitude of the work done by the isothermal process is greater than the magnitude of that done by the adiabatic process. Since 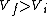 , we know both values are positive. Thus , we know both values are positive. Thus  -- (E). -- (E).
|
yosun
2005-11-10 22:45:39 |
hi keflavich: in case you forgot what daschaich mentioned about the PV diagrams, you can deduce that the work done by an adiabatic process is less than that of an isothermal process like this:
for the adiabatic process, one has 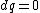 , then from the first law, one has , then from the first law, one has 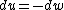 . this means that the work is path independent (since the internal energy is). so, since it's not the same as the isothermal work (due to the calculations above), the path in the PV diagram might as well curve downwards more so that the area is less. . this means that the work is path independent (since the internal energy is). so, since it's not the same as the isothermal work (due to the calculations above), the path in the PV diagram might as well curve downwards more so that the area is less.
|
partha
2006-10-30 06:13:10 |
look at the p-v diagram for both isothermal and adiabetic process...the slope of the adiabetic curve is gamma times the slope of isothermal process.Therefore between the the initial and final volume the area under the isothermal curve is greater than the adiabetic curve ...since the area under the curve gives the work done so the work done in the isothermal process is greater...it takes a few seconds to compute the answer
|
jdgayles16
2010-05-28 12:49:13 |
I thought the work of an isothermic process is negative so should it be less than zero and the work of an adiabat
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
