|
GR0177 #48
|
|
|
Problem
|
|
|
This problem is still being typed. |
Thermodynamics }RMS Speed }RMS Speed
In case one forgets the RMS speed, one does not need to go through the formalism of deriving it with the Maxwell-Boltzmann distribution. Instead, one can approximate its dependence on mass and temperature by 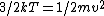 . One thus has . One thus has 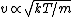 . For the ratio of velocities, one has . For the ratio of velocities, one has 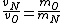 . Plug in the given molecular masses for Oxygen and Nitrogen to get choice (C). . Plug in the given molecular masses for Oxygen and Nitrogen to get choice (C).
Incidentally, the trick for memorizing the diatomic gasses is Have No Fear Of Ice Cold Beer (Hydrogen, Nitrogen, Florine, Oxygen, Iodine, Chlorine, Bromine).
|
|
|
Alternate Solutions |
asdfasdfasdf
2016-09-06 17:39:31 | Forgetting anything about 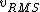 I assumed that since it\'s at constant temperature, the oxygen and nitrogen should have the same kinetic energy:\r\n I assumed that since it\'s at constant temperature, the oxygen and nitrogen should have the same kinetic energy:\r\n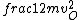 = = 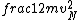 \r\n\r\n \r\n\r\n 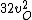 = = 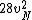 \r\n\r\n \r\n\r\n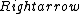 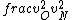 = = 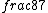 \r\n\r\n \r\n\r\n 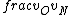 = = 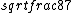 \r\n\r\n Is it just coincidental that I got the right answer for this? Or does it matter that we\'re dealing with the ratio of the \r\n\r\n Is it just coincidental that I got the right answer for this? Or does it matter that we\'re dealing with the ratio of the 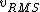 ? Or that they\'re both diatomic? ? Or that they\'re both diatomic?
asdfasdfasdf
2016-09-06 17:43:40 |
Hm, I don\'t know latex, but when I previewed my post, it looked good, I\'m not sure what happened. Here\'s my non-latex answer:\r\n\r\n(1/2)(m)(v_O)^2 = (1/2)(m)(v_N)^2\r\n\r\n==> (32)(v_O)^2 = (28)(v_N)^2\r\n\r\n==> (v_N)^2 / (v_O)^2 = (32)/(28) = (8)/(7)\r\n\r\n==> (v_N) / (v_O) = sqrt(8/7)
|
|  | uhurulol
2014-10-20 17:39:18 | This can be solved very simply by just knowing the 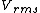 formula, formula,
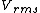 = = 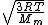
Manipulate this algebraically to find the ratio by plugging in 28 and 32 to the respective 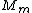 slots (remember that we're finding a ratio, so the Mass units don't really matter so long as they are consistent throughout the equation, slots (remember that we're finding a ratio, so the Mass units don't really matter so long as they are consistent throughout the equation,
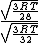 = = 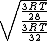 = = 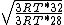 = = 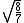
As in choice (C). Hope this simple solution helps. |  | Izaac
2012-08-30 01:06:02 | My way:
- They talk about a ratio. Log of a ratio is actually a difference: eliminate (E).
- They talk about a ROOT mean square speed, so as a hint let's consider (B) and (C) (besides those are almost the same, as if ETS was trying to trick you out of confusion).
- 5 seconds to get that 7/8 is actually 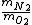 . We're looking for . We're looking for 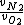 . But speed proportional to mass sounds weird, so let's take the ratio inverse. That's (C). . But speed proportional to mass sounds weird, so let's take the ratio inverse. That's (C).
As with all answers of the kind, it's not waterproof, but not so rarely it leads you to the right answer. |  |
|
|
Comments |
asdfasdfasdf
2016-09-06 17:39:31 | Forgetting anything about 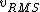 I assumed that since it\'s at constant temperature, the oxygen and nitrogen should have the same kinetic energy:\r\n I assumed that since it\'s at constant temperature, the oxygen and nitrogen should have the same kinetic energy:\r\n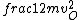 = = 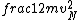 \r\n\r\n \r\n\r\n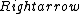 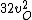 = = 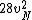 \r\n\r\n \r\n\r\n 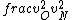 = = 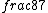 \r\n\r\n \r\n\r\n 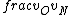 = = 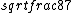 \r\n\r\n Is it just coincidental that I got the right answer for this? Or does it matter that we\'re dealing with the ratio of the \r\n\r\n Is it just coincidental that I got the right answer for this? Or does it matter that we\'re dealing with the ratio of the 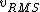 ? Or that they\'re both diatomic? ? Or that they\'re both diatomic?
asdfasdfasdf
2016-09-06 17:43:40 |
Hm, I don\'t know latex, but when I previewed my post, it looked good, I\'m not sure what happened. Here\'s my non-latex answer:\r\n\r\n(1/2)(m)(v_O)^2 = (1/2)(m)(v_N)^2\r\n\r\n==> (32)(v_O)^2 = (28)(v_N)^2\r\n\r\n==> (v_N)^2 / (v_O)^2 = (32)/(28) = (8)/(7)\r\n\r\n==> (v_N) / (v_O) = sqrt(8/7)
|
|  | uhurulol
2014-10-20 17:39:18 | This can be solved very simply by just knowing the 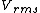 formula, formula,
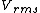 = = 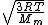
Manipulate this algebraically to find the ratio by plugging in 28 and 32 to the respective 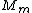 slots (remember that we're finding a ratio, so the Mass units don't really matter so long as they are consistent throughout the equation, slots (remember that we're finding a ratio, so the Mass units don't really matter so long as they are consistent throughout the equation,
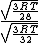 = = 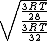 = = 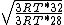 = = 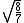
As in choice (C). Hope this simple solution helps. |  | Izaac
2012-08-30 01:06:02 | My way:
- They talk about a ratio. Log of a ratio is actually a difference: eliminate (E).
- They talk about a ROOT mean square speed, so as a hint let's consider (B) and (C) (besides those are almost the same, as if ETS was trying to trick you out of confusion).
- 5 seconds to get that 7/8 is actually 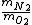 . We're looking for . We're looking for 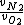 . But speed proportional to mass sounds weird, so let's take the ratio inverse. That's (C). . But speed proportional to mass sounds weird, so let's take the ratio inverse. That's (C).
As with all answers of the kind, it's not waterproof, but not so rarely it leads you to the right answer. |  | mpdude8
2012-04-20 21:23:52 | Look at things like momentum, kinetic energy, etc., mass and speed are always on the same side of the equation (i.e., inversely related). So, the more massive thing should have the slower speed, and this ratio should be greater than 1.
The fact that it's the root mean square told me there's probably square roots involved, but I had it narrowed down to two choices anyway. |  | Albert
2009-10-28 05:21:26 | Neat trick Yosun! Have No Fear Of Ice Cold Beer, loved it :) |  | theFireman
2009-09-11 21:50:00 | Also simply graham's law of effusion:
v_rms_A/v_rms_B =Sqrt(mass_B/mass_A) |  | wangjj0120
2008-11-06 20:33:25 | Wooops.
i am sorry.
I mean, Kinetic energy includs translation, rotation and vibration kinetic energy. Total energy is equal to kinetic energy and potential energy. and temperature only involves translation energy.
|  | lattes
2008-10-15 12:47:56 | instead of 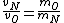 it should be it should be 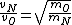 . . |  | Ning Bao
2008-02-01 06:50:39 | Smaller things go faster, but not that much fast ->C.
I love non-math physics.
a19grey2
2008-11-05 22:47:51 |
Wow, good catch. I was stupid enough to solve the problem before looking at the answers. The best advice I can give everyone is to always look at the answers before trying to do the problem.
This lets you check limits and units before wasting time. Also, it lets you know how accurate you will need to be in your calculations/approximations to narrow down the choices.
|
f4hy
2009-11-06 23:24:58 |
How does this help decide between 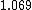 vs vs 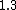 . Both to me are not that much faster. . Both to me are not that much faster.
|
|  | Mexicana
2007-09-28 17:56:58 | Just a small correction. The kinetic energy of O and N and N cannot really be approximated as cannot really be approximated as 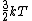 as Yosun is stating... In fact for a diatomic molecule the number of degrees of freedom is 5 and so, the energy of both O as Yosun is stating... In fact for a diatomic molecule the number of degrees of freedom is 5 and so, the energy of both O and N and N is is 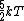 . However, this doesnt make a difference in the answer as we are asked for a ratio of rms velocities and both molecules are diatomic. This point would make a difference in the answer if for example we were dealing with a mixture of diatomic with monotic gases. . However, this doesnt make a difference in the answer as we are asked for a ratio of rms velocities and both molecules are diatomic. This point would make a difference in the answer if for example we were dealing with a mixture of diatomic with monotic gases.
Richard
2007-10-25 21:45:17 |
Thanks for pointing that out...I was about to.
Diatomic molecules have three translational degrees of freedom and two rotational degrees of freedom:
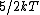
|
hayim
2008-11-05 07:20:06 |
note that at higher temperatures a diatomic molecule actually has 7 degrees of freedom contributing to its energy, the additional 2 being vibrational kinetic and vibrational potential of the internuclear bond.
i guess an 'ideal' diatomic gas ignores these 2 since they are not significant at low temperatures (ie the molecule more approximates a rigid dumbell), but at high temps these will come into play and so 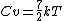
|
wangjj0120
2008-11-06 20:22:45 |
Mexicana:
your comment is not exactly correct. 5KT/2 is internal energy, which is equal to kinetic energy(3KT/2) plus potential energy(2KT/2 for rotation energy here). but temperature, (or kinetic temperature) only involves translational degree of freedom, that is kinetic energy here.
|
wangjj0120
2008-11-06 20:34:09 |
Wooops.
i am sorry.
I mean, Kinetic energy includs translation, rotation and vibration kinetic energy. Total energy is equal to kinetic energy and potential energy. and temperature only involves translation energy.
|
jmason86
2009-07-14 22:12:39 |
Word to Wang.. I was about to comment the same.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
