|
GR0177 #43
|
|
|
|
|
Alternate Solutions |
QM320
2008-11-05 20:50:33 | You can also do it by brute force:
![[L_x L_y,L_z] = L_x L_y L_z - L_z L_y L_x](/cgi-bin/mimetex.cgi?[L_x L_y,L_z] = L_x L_y L_z - L_z L_y L_x)
Using the given commutation relations, this is equal to
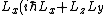-(i\hbar L_y+L_x L_z) L_y)
Rearranging and canceling gives choice (D).
Note: This was supposed to be an alternate solution, so I've reposted it as such. If someone could tell me how to delete my original (duplicate) comment, below, that would be helpful. :) |  |
|
|
Comments |
QM320
2008-11-05 20:50:33 | You can also do it by brute force:
![[L_x L_y,L_z] = L_x L_y L_z - L_z L_y L_x](/cgi-bin/mimetex.cgi?[L_x L_y,L_z] = L_x L_y L_z - L_z L_y L_x)
Using the given commutation relations, this is equal to
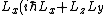-(i\hbar L_y+L_x L_z) L_y)
Rearranging and canceling gives choice (D).
Note: This was supposed to be an alternate solution, so I've reposted it as such. If someone could tell me how to delete my original (duplicate) comment, below, that would be helpful. :)
thisguy
2009-10-23 15:16:39 |
There's a small typo. [LxLy,Lz] = LxLyLz - LzLxLy. Not LxLyLz - LzLyLx as you wrote.
|
hybridusmanus
2010-06-15 18:06:16 |
Why can't re-associate the commutations after expansion? rnrni.e. rn[L L L ,L ,L ] = rnL ] = rnL L L L L - L - L L L L L =rnL =rnL (L (L L L ) - (L ) - (L L L )L )L = rnL = rnL ihL ihL - ihL - ihL L L = rnih(L = rnih(L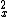 - L - L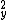 )rnrndoes this not always work? )rnrndoes this not always work?
|
walczyk
2011-04-07 08:51:16 |
Just wanted to clarify what the typo was and why it is significant. We cannot commute these orbital momentum operators willy nilly, without adding extra terms and whatnot so its a delicate procedure you could say. So beginning we have ![[L_xL_y,L_z] = L_xL_yL_z-L_zL_xL_y](/cgi-bin/mimetex.cgi?[L_xL_y,L_z] = L_xL_yL_z-L_zL_xL_y) . Let's follow the original approach and try to substitute something for . Let's follow the original approach and try to substitute something for 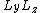 and and 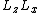 . Quickly write out . Quickly write out ![[L_y,L_z] = L_yL_z - L_zL_y = i\hbar L_x](/cgi-bin/mimetex.cgi?[L_y,L_z] = L_yL_z - L_zL_y = i\hbar L_x) , rearrange to get , rearrange to get 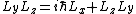 . You can keep going with it if you'd like. . You can keep going with it if you'd like.
I'm curious what happens if you try to do something different.. ![[L_x,L_y]=L_xL_y-L_yL_x=i\hbar L_z](/cgi-bin/mimetex.cgi?[L_x,L_y]=L_xL_y-L_yL_x=i\hbar L_z) , so we've got , so we've got  . .
|
|  | QM320
2008-11-05 20:49:13 | You can also do it by brute force:
![[L_x L_y,L_z] = L_x L_y L_z - L_z L_y L_x](/cgi-bin/mimetex.cgi?[L_x L_y,L_z] = L_x L_y L_z - L_z L_y L_x)
Using the given commutation relations, this is equal to
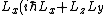-(i\hbar L_y+L_x L_z) L_y)
Rearranging and canceling gives choice (D). |  | Anastomosis
2008-04-10 14:20:54 | A quick way to do this:
As the commutator is ![[L_xL_y, L_z]](/cgi-bin/mimetex.cgi?[L_xL_y, L_z]) , ,
Use the right hand rule to point first in the +X+Y (diagonal) direction, and then curl up to the Z direction. Your thumb will be pointing in the +X-Y direction, so thus choice (D) |  | bootstrap
2007-04-06 20:15:33 | The question have it setup as [AB,C] which is [AB,C] = A[B,C] + [A,C]B. Its very similar to what is posted.. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
