|
GR0177 #29
|
|
|
|
|
Alternate Solutions |
Qubbajsara
2016-10-19 00:56:52 | Of course if you sum the probability amplitude the answer will be one\\\\r\\\\nThe right answer is that the state with the highest probability is the one with eigen value rqual to 1 and probability amplitude equal to one half so its eigen value is the expectation value (most probable value) |  | davidkaleko
2010-09-15 10:26:10 | < 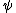 |O| |O|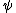 > -------- < > -------- <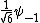 + + 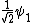 + + 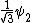 | O | | O | 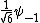 + + 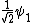 + + 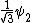 >$----------------you can separate the above out to be 9 terms, with-----------O| >$----------------you can separate the above out to be 9 terms, with-----------O|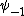 > = -1* > = -1*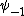 , O| , O| >=1* >=1* , O| , O|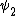 >=2* >=2*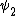 ----------------also, < ----------------also, < 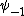 | |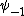 > = 1, while < > = 1, while < 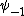 | |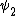 > = < > = < 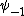 | | > = 0, due to orthogonality. This makes 6 of the 9 terms go to zero.-------------plug it all in---------------(1) > = 0, due to orthogonality. This makes 6 of the 9 terms go to zero.-------------plug it all in---------------(1)^2) + (1) + (1)^2) + (2) + (2)^2) = 1---------------------Sorry for the messy solution, I can't for the life of me figure out how to make a new line in this pseudo-latex format! = 1---------------------Sorry for the messy solution, I can't for the life of me figure out how to make a new line in this pseudo-latex format! |  |
|
|
Comments |
camarasi
2017-06-10 03:29:33 | Definition of expectation value of an operator O is\r\n\r\n< O > = < |O |O >\r\n\r\nPlugging in our state >\r\n\r\nPlugging in our state  ...\r\n\r\n< ...\r\n\r\n< |O |O > = < > = <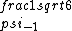 + +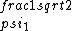 + + |O( |O(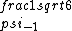 + +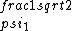 + + )>\r\n\r\nNow we \'multiply out\' the inner product. This is similar to squaring a term like (a+b+c). You will get 9 terms - messy!\r\n\r\nBut remember that \r\n\r\n< )>\r\n\r\nNow we \'multiply out\' the inner product. This is similar to squaring a term like (a+b+c). You will get 9 terms - messy!\r\n\r\nBut remember that \r\n\r\n<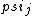 | |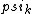 > = > = 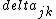 \r\n\r\nwhere \r\n\r\nwhere 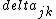 is the Kronecker delta function.\r\n\r\nSo only 3 terms survive.\r\n\r\n< is the Kronecker delta function.\r\n\r\nSo only 3 terms survive.\r\n\r\n< |O |O > = < > = <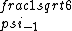 |O |O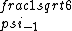 > + < > + <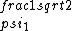 |O |O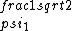 > + < > + <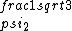 |O |O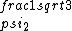 >\r\n\r\n= >\r\n\r\n=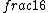 < <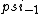 |O |O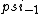 > + > + 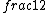 < <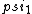 |O |O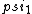 > + > + 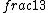 < <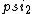 |O |O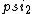 >\r\n\r\nProblem tells us that \r\n\r\n< >\r\n\r\nProblem tells us that \r\n\r\n<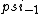 |O |O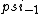 > = -1\r\n< > = -1\r\n<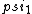 |O |O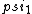 > = 1\r\n< > = 1\r\n<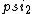 |O |O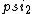 > = 2\r\n\r\nUsing these, \r\n\r\n< > = 2\r\n\r\nUsing these, \r\n\r\n< |O |O > = - > = -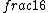 + + 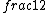 + + 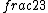 = 1\r\n\r\nAnswer: (C)\r\n = 1\r\n\r\nAnswer: (C)\r\n |  | camarasi
2017-06-10 03:07:40 | Definition of expectation value of an operator O is \r\n\r\n 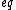 < < |O |O >\r\n\r\n >\r\n\r\n |  | Qubbajsara
2016-10-19 00:56:52 | Of course if you sum the probability amplitude the answer will be one\\\\r\\\\nThe right answer is that the state with the highest probability is the one with eigen value rqual to 1 and probability amplitude equal to one half so its eigen value is the expectation value (most probable value) |  | davidkaleko
2010-09-15 10:26:10 | < 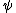 |O| |O|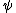 > -------- < > -------- <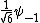 + + 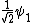 + + 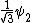 | O | | O | 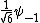 + + 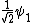 + + 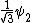 >$----------------you can separate the above out to be 9 terms, with-----------O| >$----------------you can separate the above out to be 9 terms, with-----------O|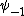 > = -1* > = -1*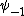 , O| , O| >=1* >=1* , O| , O|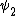 >=2* >=2*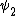 ----------------also, < ----------------also, < 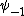 | |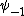 > = 1, while < > = 1, while < 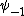 | |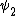 > = < > = < 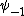 | | > = 0, due to orthogonality. This makes 6 of the 9 terms go to zero.-------------plug it all in---------------(1) > = 0, due to orthogonality. This makes 6 of the 9 terms go to zero.-------------plug it all in---------------(1)^2) + (1) + (1)^2) + (2) + (2)^2) = 1---------------------Sorry for the messy solution, I can't for the life of me figure out how to make a new line in this pseudo-latex format! = 1---------------------Sorry for the messy solution, I can't for the life of me figure out how to make a new line in this pseudo-latex format! |  | davidkaleko
2010-09-15 10:20:04 | < 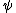 |O| |O|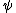 >rnrn< >rnrn<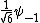 + + 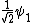 + + 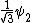 | O | | O | 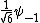 + + 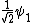 + + 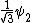 >rnyou can separate the above out to be 9 terms, withrnrnO| >rnyou can separate the above out to be 9 terms, withrnrnO|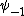 > = -1* > = -1*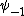 rnO| rnO| >=1* >=1* rnO| rnO|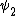 >=2* >=2*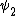 rnrnalso, < rnrnalso, < 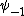 | |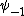 > = 1, while < > = 1, while < 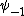 | |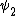 > = < > = < 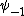 | | > = 0, due to orthogonality. This makes 6 of the 9 terms go to zero.rnrnplug it all inrnrn(-1) > = 0, due to orthogonality. This makes 6 of the 9 terms go to zero.rnrnplug it all inrnrn(-1)^2) + (1) + (1)^2) + (2) + (2)^2) = 1 = 1 |  | diane
2010-01-05 20:42:25 | 1/6+1/2+2/3= (1+3+4)/6=8/6=4/3
so what gives?
Professor
2010-01-12 11:55:53 |
It is NOT 1/6, it is -1/6.
|
|  | lathena
2009-10-08 21:31:41 | Hi,
Further clarification on this problem would be nice. Why are the square rooted parts squared?
lathena
2009-10-08 21:57:23 |
err, ignore this. I thought about it more and it made sense.
|
buaasyh
2015-08-25 11:55:46 |
The coefficients of the orthogonal base states represent the probability amplitude to be in those states. The probability to be in those states are conjugate squares of the amplitudes. Because the amplitudes are real, the coefficients are squared to make the probabilities.
|
|  |
|
| Post A Comment! |
You are replying to:
Definition of expectation value of an operator O is\r\n\r\n< O > = <  |O  >\r\n\r\nPlugging in our state  ...\r\n\r\n<  |O  > = < 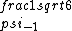 + 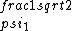 +  |O( 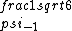 + 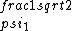 +  )>\r\n\r\nNow we \'multiply out\' the inner product. This is similar to squaring a term like (a+b+c). You will get 9 terms - messy!\r\n\r\nBut remember that \r\n\r\n< 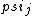 | 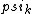 > = 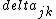 \r\n\r\nwhere 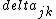 is the Kronecker delta function.\r\n\r\nSo only 3 terms survive.\r\n\r\n<  |O  > = < 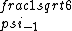 |O 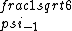 > + < 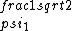 |O 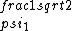 > + < 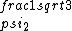 |O 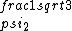 >\r\n\r\n= 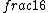 < 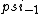 |O 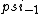 > + 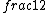 < 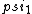 |O 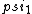 > + 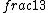 < 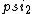 |O 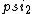 >\r\n\r\nProblem tells us that \r\n\r\n< 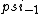 |O 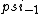 > = -1\r\n< 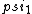 |O 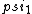 > = 1\r\n< 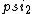 |O 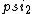 > = 2\r\n\r\nUsing these, \r\n\r\n<  |O  > = - 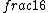 + 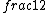 + 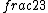 = 1\r\n\r\nAnswer: (C)\r\n |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 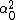 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
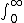 |
| $\partial$ |
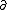 |
| $\Rightarrow$ |
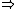 |
| $\ddot{x},\dot{x}$ |
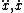 |
| $\sqrt{z}$ |
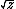 |
| $\langle my \rangle$ |
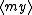 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
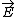 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
