GREPhysics.NET: GR0177 #23

GR0177 #23

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Mechanics $\Rightarrow$ }Vectors

If a particle is moving in a circle, then its acceleration points towards the center---even if it is moving at a constant (magnitude) velocity. This is the normal component of acceleration.

Now, if its tangential velocity is increasing, then it has a tangential acceleration. The tangential acceleration is given as just $a_t=10 m/s^2$ .

The normal acceleration is given by the centripetal acceleration formula $a_n=v^2/r = 100^2/10=10$ .

Vectorially add the normal and tangential acceleration and dot it with the tangential velocity to find that the angle between them is just 45 degrees.

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

secretempire1
2012-08-28 08:07:17

It's rather easy to visualize this problem.

You have a particle moving tangentially to the orbit at 10m/s.

Simply being constrained to this orbit gives it a centripetal acceleration equal to 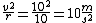$\frac{v^2}{r} = \frac{10^2}{10}=10 \frac{m}{s^2}$ , that points inward radially.

The problem also states that the particle's speed is increasing (tangentially) at 10 m/s². This gives us two acceleration vectors, one pointing radially inward with a magnitude of 10, and one tangentially (making each vector at 90 degrees to each other) with a magnitude of 10. Two equal vectors at 90 degrees to each other yields a vector at 45 degrees. Therefore, the angle between the tangent and the 45 degree acceleration vector is just 90-45 = 45.

Reply to this comment

f4hy
2009-04-02 15:05:26

Looks like there is a typo. It should read 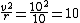$\frac{v^2}{r}=\frac{10^2}{10} = 10$ . You squared the velocity but left the squared symbol.

Reply to this comment

senatez
2006-11-02 12:36:28

The accellaration vector will be a vector with equal magnitude along the tangent and normal direction, so it will be along the 45 degree angle. I dont think a dot product is necessary to "see" the angle.

Reply to this comment

tachyon
2005-11-11 08:56:30

I think you meant to say "Vectorially add the normal and tangential ACCELERATION", not the velocity.

I really appreciate the website, since I'm taking the test tomorrow!!(if I hadn't said so in previous posts)

yosun
2005-11-11 14:17:59

tachyon: yes, that's what i meant; i was conjuring up solutions on the fly, typing as fast as i could, from the illegible stuff i jotted down when i took the test for practice. thanks for the typo-alert; it's been corrected.

Reply to this comment

Post A Comment!

You are replying to:

It's rather easy to visualize this problem. You have a particle moving tangentially to the orbit at 10m/s. Simply being constrained to this orbit gives it a centripetal acceleration equal to $\frac{v^2}{r} = \frac{10^2}{10}=10 \frac{m}{s^2}$ , that points inward radially. The problem also states that the particle's speed is increasing (tangentially) at 10 m/s². This gives us two acceleration vectors, one pointing radially inward with a magnitude of 10, and one tangentially (making each vector at 90 degrees to each other) with a magnitude of 10. Two equal vectors at 90 degrees to each other yields a vector at 45 degrees. Therefore, the angle between the tangent and the 45 degree acceleration vector is just 90-45 = 45.

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone