A more appropriate solution would be:
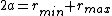
, where

is the semimajor axis. This elimiates choice (E).
The angular momentum of the moon is conserved because there are no external torques. Therefore
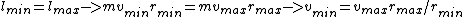
, where
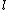
is the magnitude of the angular momentum, and
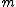
is the mass of the moon. This eliminates choice (C).
Since there is no external work being done on or by the moon, the mechanical energy of the moon is conserved. Also, since the potential energy of the moon goes as
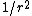
, the potential energy is minimal at
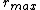
and maximal at
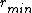
. Thus, the kinetic energy (and therefore the velocity) is maximal at
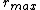
and minimal at
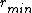
. With the
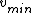
now known (as explained in the previous paragraph), the mass of the planet,
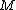
, can be calculated using the conservation of energy:
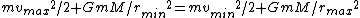
. Note again that
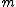
cancels. This eliminates choice (B).
Now that the mass of the planet is known, the period,

, can be calculated using Kepler's third law:
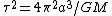
. This eliminates choice (D).
Only choice (A) remains.
