amber
2014-10-22 17:33:43 | I just remembered SPUTNIK.
The Soviet Union launched it and we couldn't figure out its mass. |  | Ning Bao
2008-02-01 06:11:15 | Consider the asteroid belt. They're not all the same size. Thus, their orbits are not determined by masses, because certainly in the muck there are a few asteroids of wildly varying size with very similar orbits. |  | KarstenChu
2007-03-22 14:03:05 | It's possible, it seems, to just look at the case of a circular orbit. Setting GMm/r^2=mv^2/r reveals that m cancels out....no mass of the moon for you! |  | travis.nicholson
2006-10-23 01:49:09 | A more appropriate solution would be:
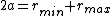 , where , where  is the semimajor axis. This elimiates choice (E). is the semimajor axis. This elimiates choice (E).
The angular momentum of the moon is conserved because there are no external torques. Therefore 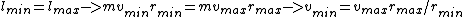 , where , where 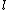 is the magnitude of the angular momentum, and is the magnitude of the angular momentum, and 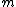 is the mass of the moon. This eliminates choice (C). is the mass of the moon. This eliminates choice (C).
Since there is no external work being done on or by the moon, the mechanical energy of the moon is conserved. Also, since the potential energy of the moon goes as 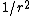 , the potential energy is minimal at , the potential energy is minimal at 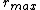 and maximal at and maximal at  . Thus, the kinetic energy (and therefore the velocity) is maximal at . Thus, the kinetic energy (and therefore the velocity) is maximal at 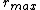 and minimal at and minimal at  . With the . With the 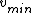 now known (as explained in the previous paragraph), the mass of the planet, now known (as explained in the previous paragraph), the mass of the planet,  , can be calculated using the conservation of energy: , can be calculated using the conservation of energy:
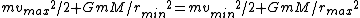 . Note again that . Note again that 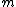 cancels. This eliminates choice (B). cancels. This eliminates choice (B).
Now that the mass of the planet is known, the period,  , can be calculated using Kepler's third law: , can be calculated using Kepler's third law:
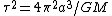 . This eliminates choice (D). . This eliminates choice (D).
Only choice (A) remains. |  | travis.nicholson
2006-10-23 01:40:58 | A more appropriate solution would be:
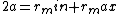 , where , where  is the semimajor axis. This elimiates choice (E). is the semimajor axis. This elimiates choice (E).
The angular momentum of the moon is conserved because there are no external torques. Therefore 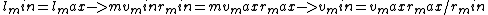 , where , where 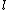 is the magnitude of the angular momentum, and is the magnitude of the angular momentum, and 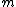 is the mass of the moon. This eliminates choice (C). is the mass of the moon. This eliminates choice (C).
Since there is no external work being done on or by the moon, the mechanical energy of the moon is conserved. Also, since the potential energy of the moon goes as 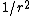 , the potential energy is minimal at , the potential energy is minimal at 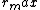 and maximal at and maximal at 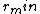 . Thus, the kinetic energy (and therefore the velocity) is maximal at . Thus, the kinetic energy (and therefore the velocity) is maximal at 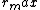 and minimal at and minimal at 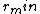 . With the . With the 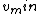 now known (as explained in the previous paragraph), the mass of the planet, now known (as explained in the previous paragraph), the mass of the planet,  , can be calculated using the conservation of energy: , can be calculated using the conservation of energy:
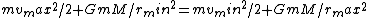 . Note again that . Note again that 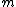 cancels. This eliminates choice (B). cancels. This eliminates choice (B).
Now that the mass of the planet is known, the period,  , can be calculated using Kepler's third law: , can be calculated using Kepler's third law:
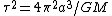 . This eliminates choice (D). . This eliminates choice (D).
Only choice (A) remains.
travis.nicholson
2006-10-23 01:50:57 |
Sorry ... for some reason when I attempted to fix the syntax in this solution the page would not allow me to submit the edited version. Therefore, I posted the solution again.
|
|  |
|
