|
GR0177 #1
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Acceleration Vector }Acceleration Vector
This is a conceptual vectors problem.
Tangential: One knows that the velocity of the bob at the endpoints is 0, and that it has maximal acceleration (pulling it back towards the center) at the endpoints. In the center, it has maximal velocity and thus minimal acceleration.
Normal: The normal acceleration varies from 0 at the endpoints to its maximal value at the center. The normal acceleration varies so that the sum of tangential and normal accelerations is a constant.
|
|
|
Alternate Solutions |
ppugpug
2010-01-31 19:42:39 | I use this idea
sigma 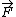 = m = m 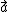 = = 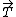 + + 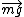
find out 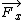 and and 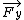 (each position) (each position)
direcion will appear
answer (C) |  | wangjj0120
2008-10-24 21:12:18 | Yosun's statement is almost correct, except the last sentence. In fact, the magnitude of acceleration varies!
You can see the physics from 9277.93, at
http://grephysics.net/ans/9277/93
At the center, 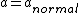 which is maximum, and which is maximum, and 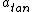 =o there. =o there.
From endpoints to center, 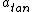 is decreasing, however, is decreasing, however, 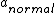 is increasing is increasing
|  | nitin
2006-11-13 11:20:02 | Your argument is wrong.
One simple way to solve this is to mentally add the forces that act on the bob at each point, which are the tension in the string and gravity (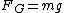 ). The only diagram that provides the right picture is (C). ). The only diagram that provides the right picture is (C). |  |
|
|
Comments |
Quark
2012-02-07 16:40:57 | My advice to those who are picking their brain over this is: The question asks you to pick the diagram that BEST illustrates the acceleration vector at each point... If you add up the tension and the gravitational force, you get the direction of the acceleration. Whether or not C is completely correct in the proportional sizes of the acceleration vectors doesn't really matter because its the BEST illustration of the acceleration vector. The others can be eliminated from common sense and symmetry. You are wasting your time on the test if you spend more than 20 seconds on this problem! |  | krazy
2011-08-12 02:04:55 | plzzzzzzzzzz help me ...... y problem statement are missing in 0177 and 9677.................??? only solutions ....
bcomnes
2011-09-16 11:59:37 |
Google for a copy of the test. It is not hard to find.
|
|  | krazy
2011-08-11 03:16:08 | where is the statement???? only solution wd out statment of the problem.............. |  | mbb_chitsazi@yahoo.com
2011-04-06 02:26:20 | |  | sina
2010-10-05 09:08:09 | You can easily eliminate down to C and E by symmetry arguements.
Then, first consider orbital motion in a plane. Force is always radial and so acceleration is always radial. In pendulum we have got both radial force that is tension and E corresponds to a orbital motion with out gravity. C is the true answer that is radial acceleration plus the effect of gravity. |  | BerkeleyEric
2010-07-11 16:13:20 | Here we have 1) centripetal acceleration and 2) a constant downward acceleration from gravity.
So at the center of the motion the vector can only be up or down. This eliminates A, B, and D. Adding the gravity contribution to the acceleration at the non-center points should change the direction of the vector, so this eliminates E. |  | ppugpug
2010-01-31 19:42:39 | I use this idea
sigma 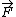 = m = m 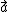 = = 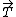 + + 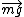
find out 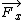 and and 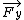 (each position) (each position)
direcion will appear
answer (C) |  | 4maitland
2009-11-06 12:30:00 | Oh boy, I am not ready for this exam 11/007/2009!
Wish I could say I have confidence but I don't. be lucky to get a 450!
fiber
2009-11-07 03:58:42 |
Quite the same... 1.5H until exam time and I still don't feel ready!
|
|  | wangjj0120
2008-10-24 21:12:18 | Yosun's statement is almost correct, except the last sentence. In fact, the magnitude of acceleration varies!
You can see the physics from 9277.93, at
http://grephysics.net/ans/9277/93
At the center, 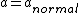 which is maximum, and which is maximum, and 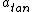 =o there. =o there.
From endpoints to center, 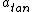 is decreasing, however, is decreasing, however, 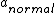 is increasing is increasing
wangjj0120
2008-10-24 21:15:26 |
btw~
yosun, thanks !! your website is great and help me a lot~
|
|  | pariahboy
2008-08-21 09:10:41 | The problem is simple:
1) the vectors are net acceleration vectors.
2) consider the endpoints and the middle. A is wrong else the point wont return to center, B is obviously velocity vectors, C we will get back to in a second, D like B are velocity vectors, E is the other option.
3) If E is what you are considering, how does the point drop to d from e if e has no net downward acceleration? it can't, C can because it has a net downward acceleration so C is the answer.
nobel
2008-10-31 03:11:45 |
by ur logic (If E is what you are considering, how does the point drop to d from e if e has no net downward acceleration?) C shud be wrong, since at the center there is no force to the left or right, in order to take it to the next position, there is only an upward force.
|
chrisiskey
2010-03-08 22:14:25 |
No, this makes sense. At the endpoints the velocity of the bob is zero, so there is indeed a need for a nonzero acceleration for the bob to return to the center position; however, the bob has a nonzero velocity at the center position so it is not necessary for a left- or right-pointing acceleration to be present for the bob to continue in the left/right direction. Consider circular motion - a centrally-pointing force is present yet at any instant the bob is moving perpendicular to the direction of the force vector.
|
|  | sa7ar
2008-04-06 21:56:32 | How can i get the question? its said that it is still being typed! Guys, i've got the GRE on friday (12th april)
I need fast help PLEASE!
Richard Feynman
2008-08-05 15:43:43 |
Well, my reply is not fast, and its probably useless at this point. The main idea that I would use to solve this problem is that, Force acting on a body and the acceleration, caused by this force on the body, will always be on the same direction. The main forces on this problem are, Gravity always downward, and the Tension of the string, which always has a direction parallel to the string itself. So at point C, the net force will be along the string. We know that Tension has to be bigger than Gravity otherwise, the string would break. So this leaves us with options C and E. At point (a) the velocity of the pendulum should be very close to zero, and point E says that at point (a) there is a net force pointing towards the convergent point. If you stretched an elastic string, that was tied somewhere, and released it, the motion of it would resemble the one of option E, so C should be the right choice.
|
|  | petr1243
2008-04-05 22:21:19 | 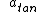 is in the same direction as the velocity of the bob when the bob is speeding up(downhill), and in opposite directions when th bob is slowing down(uphill). is in the same direction as the velocity of the bob when the bob is speeding up(downhill), and in opposite directions when th bob is slowing down(uphill). |  | nitin
2006-11-13 11:20:02 | Your argument is wrong.
One simple way to solve this is to mentally add the forces that act on the bob at each point, which are the tension in the string and gravity (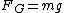 ). The only diagram that provides the right picture is (C). ). The only diagram that provides the right picture is (C). |  | scottopoly
2006-10-29 21:08:50 | In the correct answer to this problem (C), the vectors are not constant magnitude, and no reason is given in the solution above as to why that should be true.
h0dgey84bc
2007-09-16 13:59:35 |
Is there an error with this question?
Maybe they meant to say velocity vector, in which case the answer would be
(B) or (D).
(C) is almost correct, but the acceleration vector should be max at the end points not min, and it should be zero at the centre (because gravitational and tensional force cancel), also another problem with (C) is that the acceleration vector should always be tangential to the circle of motion (just resolve the graviational force into normal and tangential components, and note that the tension always cancels the normal to the circle component)
I have found applets on the web that seem to confirm this.
(A) and (E) can't possibly be correct since the velocity is definetley zero at the end points, so if the acceleration only had a normal component, the resoluting velocity would also be normal, toward or away from the centre of the circle, which is obviously not what happens.
It seems (C) is only candidate, but (C) is still erroneous.
|
marten
2007-10-29 11:52:21 |
I think (C) is not erroneous. I don't believe that the acceleration vector should be zero at the center. This is because the Tension force is greater then the gravitation force at that location. This is necessary because of the circular motion of the pendulum, so there must be a centripetal force.
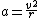
Hope that makes sense.
|
marten
2007-10-29 11:55:54 |
You can try a little experiment to perhaps convince yourself. Tie a mass to a string and compare the force of it on your hand while stationary, and spinning around in a circle. If you spin it fast, you'll notice it gets "heavy"
BTW, probably should have said centripetal acceleration, not force. The difference in forces (T-mg) provide the necessary acceleration.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
