|
GR9677 #99
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Two-State Systems }Two-State Systems
Recall the mnemonic for remembering what a LASER is---Light Amplified Stimulated Emission Radiation.
A laser consists of two states, with a metastable-state in between the top and bottom state. Initially, one has all the atoms in the ground-state. But, photons come in to excite the atoms (through absorption), and the atoms jump into the top state; this is called a population inversion, as the ground-state atoms are now mostly in the top ``inverted" state. More photons come in to excite these already excited atoms, but instead of absorption, emission occurs, and the atoms jump to a lower meta-stable state while emitting photons (in addition to the incident photons). The atoms stay in this metastable state due to selection rules, where a transition back to the ground-state is forbidden.
One doesn't need to know all that to solve this problem. Instead, merely the idea of a laser requiring two main states and a metastable state in between would suffice. Since the question gives the bottom state as 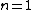 and top state as and top state as 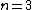 , one deduces that the metastable state must be , one deduces that the metastable state must be 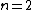 , as in choice (B). , as in choice (B).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
hanin
2009-09-30 02:46:12 | So if the transition is, for example, n=1 to n=4 then n=2 and n=3 have to be metastable? |  | casaubon
2008-10-09 00:02:30 | So I still don't get links on this site. Shows up fine in the preview. Anyways,
http://idol.union.edu/malekis/ESC24/Seyffie%27s%20Pages/Quantum%20Applications/threelevelatom.gif |  | madfish
2007-10-30 17:59:51 | I don't understand why the system must have an n=2 level, the selection rules do not forbid the electron from jumping straight from n=1, l=0, m=0 to say n=3, l=1, m=0rnwithout ever touching the n=2
Ethan
2008-10-08 19:50:28 |
I believe the explanation goes as follows: in order for a laser too work, ie amplify the light put in, there must be an excess of electrons in the high energy state. N(n=3)>N(n=1). If n=2 were not metastable then it would not be possible to maintain this excess concentration in n=3, as the electrons would fill up the n=1 level too quickly.
In multiple gas lasers (I think the most common) the active gas need not have any metastable state.
|
|  | Richard
2007-09-28 16:45:33 | Sorry to be punctilious, but "Light Amplification by Stimulated Emission" is hardly a mnemonic. It is an acronym. Do you have to remember that PHRASE to remember the word LASER? |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 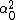 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
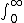 |
| $\partial$ |
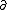 |
| $\Rightarrow$ |
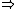 |
| $\ddot{x},\dot{x}$ |
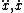 |
| $\sqrt{z}$ |
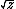 |
| $\langle my \rangle$ |
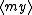 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
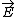 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
