|
GR9677 #73
|
|
|
|
|
Alternate Solutions |
griffitz
2012-11-07 18:57:42 | The process is adiabatic, so dQ= 0. Thus, dW = dU, or dW = f/2 * NkdT. But since T = PV/Nk, we have:
dW = f/2 * d(PV).
d(PV) = 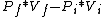
and 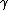 = (1+2f)/f, thus = (1+2f)/f, thus
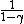 = f\2 = f\2
and we arrive at choice (C) |  |
|
|
Comments |
griffitz
2012-11-07 18:57:42 | The process is adiabatic, so dQ= 0. Thus, dW = dU, or dW = f/2 * NkdT. But since T = PV/Nk, we have:
dW = f/2 * d(PV).
d(PV) = 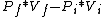
and 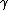 = (1+2f)/f, thus = (1+2f)/f, thus
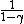 = f\2 = f\2
and we arrive at choice (C) |  | timtamm
2011-08-25 21:00:37 | i feel like there is a problem with the power in the solution to the integral it should be 1-gamma not gamma -1 in the power of V. am i crazy or is this a typo--- someone else back me up
timtamm
2011-08-25 21:01:59 |
maybe i am just forgetting that it is in the demoninator still---- god this math is driving me bananas --- i'm thinking just skipping these problems on the test
|
arboretum
2012-07-02 13:54:47 |
if you look at the problem, it asks what is the work done BY the gas. In other words, work done ON the surroundings. The expression for work is therefore going to be opposite of what it usually is (positive instead of negative).
|
arboretum
2012-07-02 13:58:17 |
oh never mind, you were asking about the 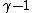 power, not the coefficient.Oops. power, not the coefficient.Oops.
|
|  | olj5
2011-08-03 08:44:15 | What is gamma=1?
olj5
2011-08-03 08:45:31 |
What IF* is what I mean.
|
pam d
2011-09-17 21:05:58 |
Gamma is the ratio of Cp to Cv, and as far as I know they are never equal. Normally the relation is Cp = Cv +R where R is the familiar gas constant. Cp is the molar heat capacity at constant pressure and Cv is the molar heat capacity at constant volume.
|
|  | archard
2010-05-30 13:30:19 | Once you see that you have an integrand 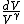 , you can pretty much bet that the answer is C since it's the only one with a , you can pretty much bet that the answer is C since it's the only one with a 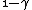 in the denominator. in the denominator. |  | Inri
2010-04-09 23:29:04 | You can immediately eliminate (D) and (E) by knowing that the numerator can't depend that way on gamma, as it produce the wrong units for anything but gamma = 0. You can immediately eliminate (A) by knowing that the work depends on the initial pressure and volume.
You can eliminate (B) by knowing that the sum of the pressures shouldn't affect the final work (though the difference might).
That leaves option (C).
Fortunately, the integral is not too difficult and in this problem you only need to get so far as the constant ) or or ) as there is only one option with that constant. as there is only one option with that constant.
flyboy621
2010-11-05 20:31:53 |
well said
|
|  | a19grey2
2008-10-30 21:07:21 | If we plug in C's dependence on V later in the problem, why can we ignore this dependence when doing the integral?
gt2009
2009-07-03 12:35:10 |
C is a constant so you can pull it out of the integral. It is not ignoring anything.
|
|  | physicsisgod
2008-10-30 15:07:48 | It took me a minute to realize how 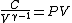 , so in case anyone else has this problem: , so in case anyone else has this problem:
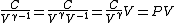
Tada! Thanks, ETS, for putting the correct answer in the most laborious form possible!
AER
2009-03-31 17:15:29 |
Thankfully, once you get the 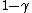 factor, you're done. factor, you're done.
|
sullx
2009-11-03 18:54:33 |
Yeah. After I saw the 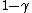 factor I was confident of C. factor I was confident of C.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
