|
GR9677 #68
|
|
|
|
|
Alternate Solutions |
jmason86
2009-10-04 15:04:26 | MOE:
As Yosun said: PE = mgscos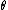 . Eliminate (B) and (C) . Eliminate (B) and (C)
Also as Yosun said: Translational KE = 1/2m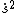 . Eliminate (D) . Eliminate (D)
Only (A) and (E) remain.
Rotational KE = something... another term. (A) is only the Translational KE and the PE; it lacks a Rotational KE term. Eliminate (A).
(E) Remains. |  |
|
|
Comments |
ngendler
2015-10-23 05:06:16 | Does no one else see a DOT over the m in choice (E)???
camcam
2019-09-12 16:14:14 |
It looks like a printing error, there are similar dots all over the page if you look closely. That one\'s just in an unfortunate spot, I guess.
|
|  | nc
2014-10-16 15:48:23 | Without actually calculating the Lagrangian, we know that kinetic energy term will depend on omega, so that eliminates A and D. We also know that L = T - U and that U = mgscos(theta). The only choice that makes sense, then, is E. |  | Sagan_fan
2013-05-23 15:08:36 | The no-effort MOE: L = T - U
Here T has two components, rotational and translational, so we want an answer with 3 terms; Eliminate (A) and (D).
Since the potential should be subtracted, eliminate (C).
By inspection, U has an angle term, eliminating (B) |  | jmason86
2009-10-04 15:04:26 | MOE:
As Yosun said: PE = mgscos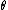 . Eliminate (B) and (C) . Eliminate (B) and (C)
Also as Yosun said: Translational KE = 1/2m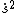 . Eliminate (D) . Eliminate (D)
Only (A) and (E) remain.
Rotational KE = something... another term. (A) is only the Translational KE and the PE; it lacks a Rotational KE term. Eliminate (A).
(E) Remains. |  | f4hy
2009-04-03 18:28:36 | LIMITS!
I first eliminated C since the wrong sign and then B because no theta dependance.
From there I thought what would happen if 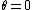 . Well then it should be like a free falling particle so D is out. The spinning must give some kinetic energy so there goes A. E is the only one left. . Well then it should be like a free falling particle so D is out. The spinning must give some kinetic energy so there goes A. E is the only one left. |  | r10101
2007-10-30 19:13:43 | After eliminating (B) and (C) by the potential term, use variable dependency: T = T) for sure, so (A) and (D) are both out as well. for sure, so (A) and (D) are both out as well.
p3ace
2008-04-11 10:25:59 |
This is a great observation, but if there were other choices with 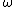 dependence in the middle term, one would have to solve more exactly. dependence in the middle term, one would have to solve more exactly.
I would use the expression for 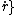 in spherical coordinates which should be memorized, and in cylindrical coord.'s as well. in spherical coordinates which should be memorized, and in cylindrical coord.'s as well.
|
p3ace
2008-04-11 10:44:23 |
I hit post prematurely. Sorry.rnAs I was saying, the expressions for velocity in the other coordinates are very handy for problems like this one because one can simply dot r vector with itself to get v^2 for kinetic energy. rnIn this case, The spherical symmetry lends itself perfectly to the problem because s is just r, and 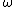 is is 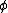 '. Also, '. Also, 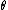 is fixed, so is fixed, so 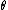 ' is zero. Then dot the velocity with itself and multiply by (1/2)m and Wah-Lah. You have it.rnI would type in the origianl expression for velocity in spherical coordinates but I'm not used to Latex and would rather be studying. I got it from Mechanics by Symon, and I've used it to solve numersous problems with cylindrical or spherical symmetry. ' is zero. Then dot the velocity with itself and multiply by (1/2)m and Wah-Lah. You have it.rnI would type in the origianl expression for velocity in spherical coordinates but I'm not used to Latex and would rather be studying. I got it from Mechanics by Symon, and I've used it to solve numersous problems with cylindrical or spherical symmetry.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 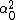 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
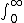 |
| $\partial$ |
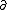 |
| $\Rightarrow$ |
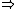 |
| $\ddot{x},\dot{x}$ |
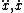 |
| $\sqrt{z}$ |
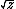 |
| $\langle my \rangle$ |
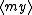 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
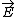 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
