|
GR9677 #49
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
syreen
2013-09-11 11:48:17 | Is it just me, or are your primes & unprimes swapped? Primed should be the moving frame, shouldn't it?
See GR8677 #22 for the same transformations, but with primes and unprimes switched.
Or does it not matter for this E&M transformations?
syreen
2013-09-11 11:50:43 |
Oops, just saw that the two are different.
Still, though, shouldn't we be solving for primed?
|
Jovensky
2013-09-23 22:18:49 |
syreen, we are looking from the rest frame of second observer, so the first observer is moving relative to the second observer, thus we are solving for the rest frame variables (the unprimed one).
|
|  | mpdude8
2012-04-20 15:09:34 | Hmm... I just said that as you increase your speed toward c, the electric field that you measure should increase.
As you increase v towards c, the square root term gets very small. Thus, it should be on the denominator. C is the only choice that has this feature -- and A should be eliminated right off the bat because it has no dependence on v in the first place. |  | wittensdog
2009-11-03 17:47:18 | I'm pretty confident that ETS is getting at the issue of length contraction here. I would say that the field transformation formulas are a nice thing to know, if you can remember them, but in my opinion understanding how length contraction and other relativistic effects come into play has more to do with the real physics going on. If you remember the formula sigma / 2*epsilon, and you realize that the charge density should go up by a factor of gamma from length contraction, you have your answer in about two seconds.
The fact that the plane is infinite means that regardless of your velocity with respect to it, you still see it as infinite, so we know we can treat the problem as an infinite plane with a different charge density.
WoolfianOperator
2009-11-05 18:27:55 |
i agree. the other options have either no effect (A) on the field or the field getting smaller because of the 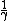 terms (B,D,E). remember gamma is always greater than or equal to 1 terms (B,D,E). remember gamma is always greater than or equal to 1
|
flyboy621
2010-10-24 16:51:33 |
good solution!
|
blairwitch
2011-03-12 09:32:24 |
could you expound on how you get (derive) sigma/2* epsilon
|
asdfuogh
2011-10-08 18:13:42 |
Great point, looking at it as if the charge density became greater due to length contraction.
|
|  | tin2019
2007-10-16 07:54:20 | I find it simpler to deal with a potential 4-vector ) which has to be invariant under Lorentz transformations. The field in question has a potential which has to be invariant under Lorentz transformations. The field in question has a potential 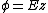 because, for using because, for using 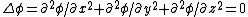 and the fact that potential must be independent of both x and y we get and the fact that potential must be independent of both x and y we get 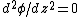 or, because or, because 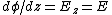 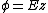 . Now applying Lorentz transformations to . Now applying Lorentz transformations to 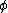 we getrnrn we getrnrn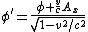 rnrnand since rnrnand since 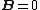 we can take the vector potential to be we can take the vector potential to be 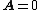 , and thus we havernrn , and thus we havernrn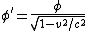 rnrnNow rnrnNow 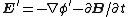 , for there is magnetic field now. , for there is magnetic field now.  component of the vector potential isrnrn component of the vector potential isrnrn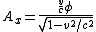 rnrnHowever this is time independent, and so our equation for electric field reduces tornrn rnrnHowever this is time independent, and so our equation for electric field reduces tornrn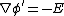 . rnrnTaking the gradient of relation . rnrnTaking the gradient of relation 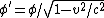 we see that the electric field in primed system must have only a we see that the electric field in primed system must have only a  component, as component, as 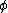 is independent of is independent of  and and 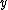 . This yieldsrnrn . This yieldsrnrn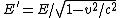 rnrnI realize that this is not the simplest solution, but it is easier for me to remember that the 4-vector is Lorentz invariant. It could be that I'm using a cannon to kill a mosquito. rnrnI realize that this is not the simplest solution, but it is easier for me to remember that the 4-vector is Lorentz invariant. It could be that I'm using a cannon to kill a mosquito.
dumbguy
2007-10-16 19:10:00 |
yeah but you killed that mosquito
|
kronotsky
2018-10-22 02:53:30 |
I think this is a lot easier than remembering how the faraday tensor transforms (thanks for the tip!), but lorentz contraction is the way to go.
|
|  | hungrychemist
2007-10-05 03:19:52 | E = sigma/2*epsilon
Consider sigma (charge density) = Q/Area = Q / X * Y but respect to second observer length in X must be shorten.
find the shorten length by X' = sqrt[1-(v/c)^2] * X
Then the new sigma is Q/(sqrt[1-(v/c)^2] * X*Y)
plug new sigma above to E equation, to get C
greenfruit
2008-11-01 10:06:03 |
awesome.
|
mike
2009-11-06 13:07:05 |
This is the best way to do it, and is a nice fact to remember
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
