|
GR9677 #35
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Identical Particles
Because of the antisymmetric interchange of identical particles, one gets 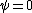 if two fermions are in the same state. This is basically the foundation behind the familiar Pauli exclusion principle.
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Skribb
2009-09-26 05:39:30 | This problem can easily be figured out by process of elimination.
(A) Recall from Gen Chem that the Pauli Exclusion Principle states that electrons with the same spin are not allowed to occupy the same location so we know this principle deals directly with the idea that electrons are fermions. Without knowing anything else, we can look at the next four and see that they are not remotely related.
(B) The Bohr Correspondence principle states that quantum mechanical equations yield classical results when subject to large numbers. This doesn't deal with the symmetry of fermions.
(C) Heisenberg's uncertainty principle states that different quantities are inversely related to one another and subject to a minimum value of certainty, momentum with position, energy with time. Again, nothing about symmetry or spin of particles.
(D) Bose Einstein condensation deals with creating a weekly interacting gas at such low temperatures to enable the gas to reach its lowest quantum state
(E) Fermi's Golden Rule describes the rate of transition between eigenstates. No spinning particles here.
By process of elimination and a rough understanding of the Pauli Exclusion principle, choose A. |  | grae313
2007-10-31 12:41:25 | In a physical chemistry class I was taught that the "smart-ass" version of the Pauli Exclusion Principle is, "electrons are fermions."
| |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
|
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
