|
GR9677 #25
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Capacitors }Capacitors
Recall the following truths (held to be self-evident?) on the subject of capacitors: 1. series capacitors have equal charge (Equivalent capacitance of two capacitors is 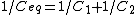 ); 2. parallel capacitance have equal voltage ( ); 2. parallel capacitance have equal voltage (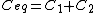 ); 3. ); 3. 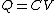 ; 4. ; 4. 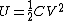 . .
(A) Initially, before the switch is closed, only 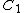 has a voltage across it, and hence it is charged. has a voltage across it, and hence it is charged. 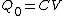 . But, afterwards, since the voltage stays the same, one has . But, afterwards, since the voltage stays the same, one has 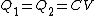 ; hence, ; hence, 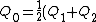) . .
(B) 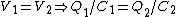 . Since . Since 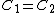 , one has , one has 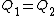 . This is true. . This is true.
(C) By definition of circuit elements in parallel, one has each capacitor at the same potential. This is trivially true. 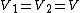
(D) Since one determined from (C) that the capacitors are at the same voltage, then because they have the same capacitance, they have the same energy as per 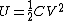 . True. . True.
(E) This is false, since 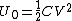 , initially. In the final state, each capacitor has energy , initially. In the final state, each capacitor has energy 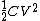 . The sum of energies is thus . The sum of energies is thus 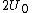 . .
|
|
|
Alternate Solutions |
kroner
2009-10-09 19:50:35 | The charged up state of a capacitor depends only on its capacitance and the voltage across it. In this case 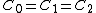 and and 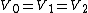 so all three are indistinguishable. So so all three are indistinguishable. So 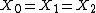 for every quantity for every quantity 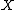 that you might measure regardless of the formulas. that you might measure regardless of the formulas. |  | jmason86
2009-09-30 17:35:59 | With Q=CV and 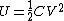 one can eliminate things pretty quickly. If C and V are the same, then Q and V must be the same as well (through the above equations). one can eliminate things pretty quickly. If C and V are the same, then Q and V must be the same as well (through the above equations).
The problem statements supplies C1 = C2.
If Q1 does happen to be equal to Q2 (i.e. answer (B)), then that means that (C) and (D) must also be true. Since we are looking for the statement that is incorrect, we can eliminate (B) (C) (D).
Charge damn well better be conserved, so you can't have Q1+Q2=Q0 or you'd be generating charge somewhere. Eliminate (A).
(E) remains. |  |
|
|
Comments |
jdbro
2014-10-23 17:43:07 | :: Careful, 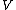 depends on depends on  . Use . Use 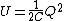 instead. instead.
|  | kroner
2009-10-09 19:50:35 | The charged up state of a capacitor depends only on its capacitance and the voltage across it. In this case 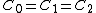 and and 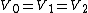 so all three are indistinguishable. So so all three are indistinguishable. So 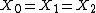 for every quantity for every quantity 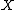 that you might measure regardless of the formulas. that you might measure regardless of the formulas. |  | dstahlke
2009-10-08 21:35:34 | Does anyone know what they mean by a "real capacitor"? Does this just mean that there is some resistance so that the wires don't melt due to the infinite amount of current that would flow otherwise? I scratched my head about this for a while before I took a look at the options and realized that the problem wasn't as hard as I was expecting it to be. |  | jmason86
2009-09-30 17:35:59 | With Q=CV and 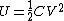 one can eliminate things pretty quickly. If C and V are the same, then Q and V must be the same as well (through the above equations). one can eliminate things pretty quickly. If C and V are the same, then Q and V must be the same as well (through the above equations).
The problem statements supplies C1 = C2.
If Q1 does happen to be equal to Q2 (i.e. answer (B)), then that means that (C) and (D) must also be true. Since we are looking for the statement that is incorrect, we can eliminate (B) (C) (D).
Charge damn well better be conserved, so you can't have Q1+Q2=Q0 or you'd be generating charge somewhere. Eliminate (A).
(E) remains.
Crandor
2010-04-09 20:04:50 |
Charge on the capacitors is not conserved; it is generated by the battery. (A) is true because C and V are the same for both capacitors, and 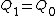 (because V didn't change). (because V didn't change). ![Q_1=Q_0=Q_2\Rightarrow Q_0=\frac{1}{2}[Q_1+Q_2]](/cgi-bin/mimetex.cgi?Q_1=Q_0=Q_2\Rightarrow Q_0=\frac{1}{2}[Q_1+Q_2])
|
|  | a19grey2
2008-10-29 15:14:46 | So, the easy way I did this was not to check for everything being true, but to look quickly for clearly False statements.
E is false because the connection of a second capacitor in parallel must add energy to the system. This is seen because capacitors in parallel must have the same Voltage and so 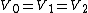 . Thus, the energy in the two capacitors is more than that in the one capacitor. . Thus, the energy in the two capacitors is more than that in the one capacitor.
This solution is nice since it doesn't even require 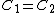
chemicalsoul
2009-10-17 01:06:19 |
I don't understand just by closing a circuit we have gained on the total energy of the system. When the circuit was open the total energy of the system was equal only to the energy stored in the charged capacitor and there wasn't any energy in the uncharged one, where did this new energy come from ?
|
carle257
2010-04-04 20:01:28 |
The battery provides additional energy when the capacitance of the circuit changed. When the switch closed, we charged up 
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
