|
GR9677 #20
|
|
|
|
|
Alternate Solutions |
homels
2016-09-08 01:51:55 | I just figure out a really fast way to do this. In this CM frame, both atoms have speed of 0.5v. After the collision, they will still have 0.5v but opposite direction. Now in lab frame, the helium atom have 0.6v, which means the lab frame is moving to the right with 0.1v with respect to CM frame. That means the velocity of surface atom should be 0.5v-0.1v=0.4v in lab frame. We know the change of momentum in this process for helium atom is 1.6*4u*v which equals to M*0.4v, then we can calculate the M out which is 16u. |  | amber
2014-10-19 10:24:28 | This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|  | socolenco
2014-08-15 11:08:06 | Conservation of Momentum:
mv = (-0.6v)m + (0.4v)M  1.6m = 0.4M 1.6m = 0.4M  M=4m=16u. M=4m=16u.
The two particles split the initial velocity in two: if the first one takes 0.6v from it, then the second remains with only 0.4v; if the first one takes 0.8v, then the second remains with only 0.2v. The momentum is conserved and the change in momentum means the change in velocity AND the conservation of momentum means the conservation of the velocity too because the mass in CM is always constant. |  | daverigie
2009-10-06 08:21:18 | When you look at an elastic collision in the center of mass frame, you can quickly realize that for momentum and energy to be conserved the particles must rebound with the same velocity that they approached one another.
Therefore the magnitude of the velocity change in the particle of mass 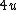 must be must be
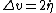
where 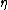 is the center of mass coordinate. is the center of mass coordinate.
v}{2} = \dot{\eta})
and
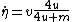
That means we need
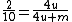
From here I would solve by inspection and realize 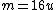
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
|  | twistor
2007-11-02 16:21:09 | Here's a quick solution:
Notice that for conservation of momentum we must have:
p = -0.6p + 1.6p and use
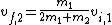 so so
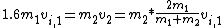
so that
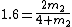
Quickly solve to find 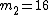
Of course it's never that easy under pressure!... Down with ETS! |  |
|
|
Comments |
homels
2016-09-08 01:51:55 | I just figure out a really fast way to do this. In this CM frame, both atoms have speed of 0.5v. After the collision, they will still have 0.5v but opposite direction. Now in lab frame, the helium atom have 0.6v, which means the lab frame is moving to the right with 0.1v with respect to CM frame. That means the velocity of surface atom should be 0.5v-0.1v=0.4v in lab frame. We know the change of momentum in this process for helium atom is 1.6*4u*v which equals to M*0.4v, then we can calculate the M out which is 16u.
arturodonjuan
2016-10-17 16:57:31 |
No, it is not true that both atoms will have the same speed in the CM frame. They will have the same momentum (by definition of the center of momentum frame, which classically is equivalent to the center of mass frame), but not the same velocity.
|
|  | amber
2014-10-19 10:24:28 | This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|  | socolenco
2014-08-15 11:08:06 | Conservation of Momentum:
mv = (-0.6v)m + (0.4v)M  1.6m = 0.4M 1.6m = 0.4M  M=4m=16u. M=4m=16u.
The two particles split the initial velocity in two: if the first one takes 0.6v from it, then the second remains with only 0.4v; if the first one takes 0.8v, then the second remains with only 0.2v. The momentum is conserved and the change in momentum means the change in velocity AND the conservation of momentum means the conservation of the velocity too because the mass in CM is always constant. |  | superlaser1
2012-04-07 19:54:06 | First I let the mass of the target be 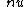 . Factors of . Factors of 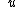 drop out of the conservation equations. Getting terms in drop out of the conservation equations. Getting terms in 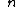 on one side of each equation yields on one side of each equation yields
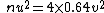
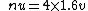
Dividing these equations gives 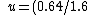v) . Thus we find the atomic number is . Thus we find the atomic number is
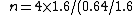=16)
which is Oxygen. The answer is D. |  | noether
2009-11-04 16:33:47 | The 'm' should not be squared under the line "from kinetic energy conservation", just the 1.6v.
noether
2009-11-04 16:35:48 |
ok nevermind
|
|  | noether
2009-11-04 16:32:55 | The 'm' should not be squared under the line "from kinetic energy conservation", just the 1.6v. |  | daverigie
2009-10-06 08:21:18 | When you look at an elastic collision in the center of mass frame, you can quickly realize that for momentum and energy to be conserved the particles must rebound with the same velocity that they approached one another.
Therefore the magnitude of the velocity change in the particle of mass 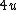 must be must be
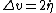
where 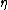 is the center of mass coordinate. is the center of mass coordinate.
v}{2} = \dot{\eta})
and
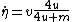
That means we need
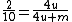
From here I would solve by inspection and realize 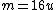
cjohnson415
2013-06-23 20:43:55 |
Can you explain how you deduce that 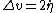 ? ?
Your solution seems much more elegant, but I am just not understanding that step in the logic. Could you possibly sketch out a derivation? Or can you at least explain the step in logic how rebounding with the same velocity yields a relationship between change in velocity and CM frame velocity?
|
cjohnson415
2013-06-23 21:06:43 |
Actually, I just realized how that follows. For others who might be wondering, here's a quick explanation:
Before the collision, particle 1 has velocity 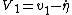 in the CM frame. In the CM frame, the two particles simply reflect off each other, keeping the same magnitude of velocities just now in opposite directions.* Thus, after the collision, particle 1 has velocity in the CM frame. In the CM frame, the two particles simply reflect off each other, keeping the same magnitude of velocities just now in opposite directions.* Thus, after the collision, particle 1 has velocity 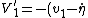 = \dot{\eta} - v_1) . But we also know that . But we also know that 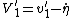 . So combining these two equations yields: . So combining these two equations yields:
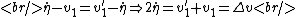
Note that 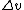 , which was defined as the change in magnitude of the velocity is equal to , which was defined as the change in magnitude of the velocity is equal to 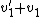 because because 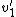 is negative. is negative.
*If you don't believe/understand the symmetry of the center of mass frame, just imagine two particles with equal momentum colliding. Regardless of the masses, of course they must bounce back in opposite directions with velocities unchanged in magnitude for the total momentum to remain zero while still conserving energy. The center of mass frame is simply the frame in which the total momentum of the two particles is zero, i.e. exactly the situation I asked you to imagine.
|
amber
2014-10-19 10:20:21 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:23:25 |
This has been great help. Thank you. Here are my 2 cents.
See page 191 of Kleppner and Kolenko. It goes step by step.
To clarify daverigie's post:
In the end you can remember that the velocity before collision in CM is
V = (m1v1 + m2v2)/(m1+m2)
The velocities after collision in CM are
v1cm = m2/(m1+m2) (v1-v2)
v2cm = -m1/(m1+m2) (v1-v2)
where v1cm and v2cm are the velocities of the particles before the collision in CM. and v1 and v2 are the velocities of the particles in LAB.
For this problem:
v1 = v and v2 = 0
before collision:
V = m1v /(m1+m2)
Since we know that
change in v = 2*V
we also get
V = change in v / 2 = (1-.6)v/2 = 2v/10
We set them equal to each other
2v/10 = m1v /(m1+m2)
for m1 = 4u
2/10 = 4u/(4u+m2)
Hope that helps
|
amber
2014-10-19 10:37:37 |
where v1cm and v2cm are the velocities of the particles **AFTER** the collision in CM. and v1 and v2 are the velocities of the particles in LAB **BEFORE**.
|
amber
2014-10-19 11:04:57 |
Sorry I got confused by the diagrams.
The velocities **BEFORE** collision in CM are
where v1cm and v2cm are the velocities of the particles **Before** the collision in CM. and v1 and v2 are the velocities of the particles in LAB **BEFORE**
Note that in an elastic collision the speed of each particle in the CM frame is the same before and after collision
|
|  | jw111
2008-11-04 23:50:50 | set 4u = 1, v = 1, (change the units)
then conservation laws, (M for mass of surface, k is the velocity)
1 = -0.6 + Mk ...........................(1)
1 = 0.6*0.6 +Mkk ..........(2)
16/10 = Mk
64/100 = Mkk
so k = 64*10 / 16*100 = 4/10
so M = 16*10 / 10*4 = 4
recover the unit M = 4*4u = 16u |  | tinytoon
2008-10-05 10:36:00 | I find that the most important thing to remember for elastic collisions is the formula for the relative velocities:
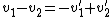
Using this formula and conservation of momentum immediately gives the answer without much work. |  | twistor
2007-11-02 16:21:09 | Here's a quick solution:
Notice that for conservation of momentum we must have:
p = -0.6p + 1.6p and use
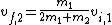 so so
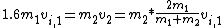
so that
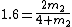
Quickly solve to find 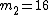
Of course it's never that easy under pressure!... Down with ETS!
blah22
2008-02-14 11:24:27 |
Type in the first formula there, that factor of 2 should be on top, no?
Also...I solved it with the other elastic eqn:
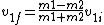
No need to worry about conservation of momentum, just solve for m2 directly. But may be a bit more algebra, depends on preference I suppose.
|
WoolfianOperator
2009-11-02 18:48:11 |
You mean solve for 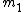 , if you solve for , if you solve for 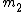 using using 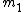 =4u one gets 1u. Which doesn't make a whole lot of sense. The equation you are using has =4u one gets 1u. Which doesn't make a whole lot of sense. The equation you are using has 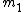 as the mass at rest not as the mass at rest not 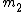
|
2010-03-26 12:28:25 |
Note that 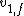 is -ve compared to is -ve compared to 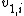 . Plug everything in the equation relating the two velocities and one gets . Plug everything in the equation relating the two velocities and one gets 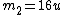 . .
|
drunkphysics
2013-09-21 11:54:58 |
hear, hear!!
|
dipanshugupta
2017-03-29 08:55:09 |
WoolfianOperator, you used 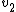 as as 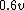 when you should\\\\\\\'ve used it as when you should\\\\\\\'ve used it as 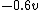 , since the He atom is travelling in the opposite direction after collision. , since the He atom is travelling in the opposite direction after collision.
|
|  | rreyes
2005-11-27 08:39:38 | It may be helpful to memorize the formula valid for elastic collisions. If initial velocity of \"target\" particle is zero, the final velocity of incoming particle is simply given by ![[(m_{inc}-m_{tar})/(m_{inc}+m_{tar})]v_{inc,init}](/cgi-bin/mimetex.cgi?[(m_{inc}-m_{tar})/(m_{inc}+m_{tar})]v_{inc,init}) . One can then solve for . One can then solve for 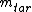 or check each choice- whichever is faster. or check each choice- whichever is faster.
Richard
2007-09-25 09:52:31 |
What you really want is the final velocity of the initially stationary particle:
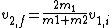
Using this and conservation of momentum, the solution comes out painlessly as 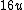 . .
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
