|
GR9677 #17
|
|
|
Problem
|
|
|
This problem is still being typed. |
Quantum Mechanics }Probability }Probability
The careless error here would be to just directly square the grids. When one remembers the significance of the meaning of the probability 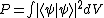 , one finds that one must square the wave function, and not the grids. , one finds that one must square the wave function, and not the grids.
The total probability is,
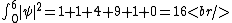
The un-normalized probability from 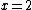 to to 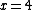 is, is,
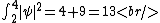
The normalized probability is thus 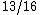 , as in choice (E). , as in choice (E).
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
mhazelm
2008-09-08 12:05:19 | If you are familiar with probability theory, this amounts to computing the probability of event A, where A is the the particle's being between x =2 and x=4. From probability, this is given as
P(A) = # ways A can occur/# total possible outcomes.
Now # ways A can occur: if x is between 2 and 3 (an interval of 1) then Psi takes on the value 2 (so Psi^2 = 4). If x is between 3 and 4 (another interval of 1), then Psi^2 = 9. Thus # ways A can occur = 4+9 = 13.
Now for the total number of possibilities, we just do the same thing, but for all possibilities of x. Our intervals are all 1, so we get
1(1^2) + 1(1^2) +1(2^2) + 1(3^2) + 1(1^2) = 16. Now just use the fact that P(A) = 13/16 and you're done with answer E being correct. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
