|
GR9677 #11
|
|
|
Problem
|
|
|
This problem is still being typed. |
Atomic }Stern-Gerlach }Stern-Gerlach
Recall the Stern-Gerlach experiment, where (in its original set-up) a beam of neutral silver atoms are sent through an inhomogeneous magnetic field. The beam's split into two---classically, from the Lorentz force, one wouldn't expect anything to happen since all the atoms are neutral, but if one accounts for the Larmor precession, one would expect the beam to be deflected into a smear. Instead, however, the beam deflects into 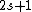 beams, and thus this supports the idea that electrons are of spin-1/2. (Ag has one unpaired electron in its beams, and thus this supports the idea that electrons are of spin-1/2. (Ag has one unpaired electron in its 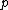 orbital.) orbital.)
With a beam of hydrogen atoms, one should also get a split into two, since 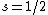 from the electron. from the electron.
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
oxide
2018-10-18 06:28:44 | okay maybe this is being picky, but I got this wrong because I considered the hyperfine structure of hydrogen, for which the lowest energy state is always a spin down electron (and proton for that matter). To be fair, in this case the beam would be deflected down, so (A) does not work either. But beware, when people refer to the ground state of hydrogen, they generally mean any of the four \\\\\\\"ground states,\\\\\\\" the triplet states and singlet state, on equal footing. |  | anuradha wijesinghe
2018-09-10 04:03:20 | why isn\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\'t the spin of the proton given any consideration ?
Batman
2018-09-13 09:06:44 |
Rotation of electron in its orbital creates a magnetic moment that interacts with the inhomogeneous magnetic field. The magnetic moment of a proton is very small compared to that of electron and hence negligible in this case. \\\\r\\\\nHowever, we have methods to work with the nuclear magnetic moment too.
|
|  | epuma
2013-06-24 19:00:40 | Ag has one unpaired electron in the 5s orbital, not in its p orbital as the original solution states. |  | PorcelainMouse
2008-11-07 12:11:16 | http://en.wikipedia.org/wiki/Stern-Gerlach |  | caffeinated
2008-04-09 15:39:26 | So why verticle? Is it because the spin axis aligns up or down with the field?
wakkadojo
2008-09-04 17:58:23 |
The idea is that the vertical  axis is arbitrary. Furthermore, axis is arbitrary. Furthermore, 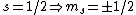 . Thus the arbitrary magnetic . Thus the arbitrary magnetic  component, in this case it can be observed parallel to the localized magnetic field, either forces the atom up or down. This is where the inhomogeneous magnetic field matters: the different spins will have different magnetic dipoles, thus if the magnetic field is inhomogeneous then the dipole will not experience a symmetric, self-canceling force, causing the beam to split into two dipole classes (i.e. component, in this case it can be observed parallel to the localized magnetic field, either forces the atom up or down. This is where the inhomogeneous magnetic field matters: the different spins will have different magnetic dipoles, thus if the magnetic field is inhomogeneous then the dipole will not experience a symmetric, self-canceling force, causing the beam to split into two dipole classes (i.e. 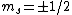 ). ).
|
wakkadojo
2008-09-04 18:23:23 |
The idea is that the vertical  axis is arbitrary. Furthermore, axis is arbitrary. Furthermore, 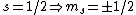 . Thus the arbitrary magnetic . Thus the arbitrary magnetic  component, in this case it can be observed parallel to the localized magnetic field, either forces the atom up or down. This is where the inhomogeneous magnetic field matters: the different spins will have different magnetic dipoles, thus if the magnetic field is inhomogeneous then the dipole will not experience a symmetric, self-canceling force, causing the beam to split into two dipole classes (i.e. component, in this case it can be observed parallel to the localized magnetic field, either forces the atom up or down. This is where the inhomogeneous magnetic field matters: the different spins will have different magnetic dipoles, thus if the magnetic field is inhomogeneous then the dipole will not experience a symmetric, self-canceling force, causing the beam to split into two dipole classes (i.e. 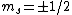 ). ).
|
wakkadojo
2008-09-04 18:33:24 |
The idea is that the vertical  axis is arbitrary. Furthermore, axis is arbitrary. Furthermore, 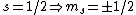 . Thus the arbitrary magnetic . Thus the arbitrary magnetic  component, in this case it can be observed parallel to the localized magnetic field, either forces the atom up or down. This is where the inhomogeneous magnetic field matters: the different spins will have different magnetic dipoles, thus if the magnetic field is inhomogeneous then the dipole will not experience a symmetric, self-canceling force, causing the beam to split into two dipole classes (i.e. component, in this case it can be observed parallel to the localized magnetic field, either forces the atom up or down. This is where the inhomogeneous magnetic field matters: the different spins will have different magnetic dipoles, thus if the magnetic field is inhomogeneous then the dipole will not experience a symmetric, self-canceling force, causing the beam to split into two dipole classes (i.e. 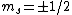 ). ).
|
maxdp
2013-09-24 16:02:29 |
I think wakkadojo overcomplicated it a bit. The particles are deflected vertically because the potential energy of a magnetic dipole moment in a magnetic field is the dot product of the dipole with the field, and the force on a particle will be the derivative of the potential energy (ignoring signs). Since the field was inhomogeneous (essential!), the derivative of the potential energy is not zero, but rather points up or down at any given point. The particle is then deflected up or down based on the sign of its spin.
If you expected a horizontal deflection, you may have used the right hand rule, but that only applies to the classical lorentz force, i.e. to a cross product. Here we have a dot product instead.
A helpful source:
http://hyperphysics.phy-astr.gsu.edu/hbase/spin.html#c5
|
|  | tareq
2007-09-26 06:35:02 | Waht about the spin of the proton ?
kyros
2007-11-02 18:47:02 |
I wondered that too - the reason we don't count it is that it's a small deviation, the gyromagnetic ratio of the proton is much much lower, and hence so is the magnetic moment of the proton, hence the hamiltonian only changes slightly due to proton spin, when compared to the electron.
|
maxdp
2013-09-24 16:43:12 |
To clarify what kyros said:
The magnetic moment is related to the spin by a factor of (q/2m). Since the proton mass is huge compared to the electron mass, its magnetic moment isn't noticed in a magnetic field.
Interestingly, the hydrogen atom as a whole still has spin of 1. It's only in a magnetic field that its effective spin becomes 1/2.
Found this explanation on this forum:
http://www.physicsforums.com/showthread.php?t=255838
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
