|
GR9277 #90
|
|
|
|
|
Alternate Solutions |
cailh
2006-10-31 07:15:01 | A simpy way. Rotational energy of di-moleculars due to far infard ray emission. Lamda approx 1*E-3 m.
Other quits:
vibration Lamada approx 1*E-6 m |  |
|
|
Comments |
enterprise
2018-03-31 21:08:51 | You can quickly notice that the MeV range is out. 10^-9 is too small. 10 ev ~ Hydrogen ionization energy which is UV. The only sensible choice is the milli ev range. |  | jondiced
2010-11-09 17:22:12 | Ground state of hydrogen's electron levels is 13.6 eV, so the rotational levels must be lower than that. This eliminates C, D, and E.
neon37
2010-11-12 08:02:26 |
why lower?
|
postal1248
2013-10-02 16:52:11 |
As nyuko says below, electronic levels are of greater energy than rotational levels.
|
|  | apps00
2010-10-06 22:32:17 | It may be useful to remember that
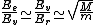
where 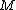 is mass of a molecula and is mass of a molecula and 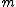 is the electron's mass. is the electron's mass. 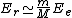 , , 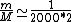 and and 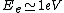
bili
2011-11-03 02:04:02 |
Wow, what a great piece of information about online dating websites. I loved it. Online dating has been my passion and I am sure I will have this opportunity to read more about online dating, dating and dating websites.
Premium " target="_blank">http://www.killerlinkx.com/">Premium Web Directory
|
syreen
2013-09-18 16:45:55 |
To the spambot (bili) who also commented on this:
A site for physicists who are busy getting ready for the GRE may be one of the least effective places to advertise for online dating I have ever seen.
|
onlinedater
2017-10-20 00:52:05 |
OMG! This is crazy. You are NOT going to believe this, bili. I also came here for online dating and was absolutely ecstatic when I discovered that the solution to my lonely single existence was #90 from 1992. Granted I\'m three years younger, 1995, but I have looked through literally 400 solutions and you are the only one I can see as a possible match so uhh you wanna maybe like I don\'t know maybe date? Only online of course. Maybe we could go to a chat room? Do you Skype? I love Skype. We should Skype. I\'m not creepy I swear. Tits or GTFO though
|
|  | BerkeleyEric
2010-06-27 23:11:52 | The thermal energy at room temp. is 1/40 eV, and these rotational energy levels are definitely accessible at that temp., so C, D, and E are eliminated. The value in A is really, really small, so we're left with B.
syreen
2013-09-18 16:16:32 |
I like this! I would add (if this works)
Each degree of freedom contributes 1/2 kT to the energy, so spacing~1/2 kT. kT at room temp~1/40 eV.
1/2(1/40)=1/8*10^-2~~10^-3.
|
|  | nyuko
2009-10-30 22:16:26 | I think it is worthwhile to know this:
Electronic levels: ~1 eV
Vibrational levels: ~0.1eV
Rotational levels: ~0.001eV
One can find this in Taylor's Modern Physics, summary for chapter 12 |  | FortranMan
2008-10-11 17:00:22 | ...I just used fNkT/2, with N =1 and T = 300K, though you did have to know what k is in eV, which the reference sheet doesn't list. Is this a no-no answer or it is okay since most of thermodynamics consists of approximations of quantum mechanical behaviors?
Poop Loops
2008-10-25 20:07:23 |
I'd say it's probably better, since you're thinking of a spinning rod. I find it kind of dubious to add the angular momenta of each particle and say that's the total angular momentum for the system. You're no longer thinking of one particle, but two together attached together...
It's like the angular momentum of Earth about its own axis and the Sun about its own axis *doesn't* give the total angular momentum of the Earth-Sun system.
|
john77
2009-03-21 07:59:46 |
This is the easiest way . And you don't have to know k in eV since your are given k in joules and the electron charge .
|
|  | cailh
2006-10-31 07:15:01 | A simpy way. Rotational energy of di-moleculars due to far infard ray emission. Lamda approx 1*E-3 m.
Other quits:
vibration Lamada approx 1*E-6 m
madfish
2007-11-01 21:28:34 |
This solutions yields order magnitude of 1 for E=h*c/lambda...doesnt seem to work
|
Jeremy
2007-11-03 15:03:55 |
I thought about it from a spectroscopy perspective as well. Recall the ever useful formula: 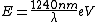 . In words, the recipe is: take 1240, divide by a wavelength in nanometers, and get an energy in electron-volts. Couple this with the fact that the energy level spacing has infra-red energies, and you quickly arrive at the correct answer. . In words, the recipe is: take 1240, divide by a wavelength in nanometers, and get an energy in electron-volts. Couple this with the fact that the energy level spacing has infra-red energies, and you quickly arrive at the correct answer.
When I first worked this problem, I wasn't too sure what wavelength range infra-red corresponded to, but I knew that red is about 600 nm, or ~2 eV. Thus, the energies in answer choices (C), (D), and (E) are far too large. 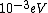 implies a wavelength of roughly implies a wavelength of roughly 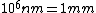 , whereas , whereas 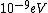 implies a wavelength one million times larger, i.e. implies a wavelength one million times larger, i.e. 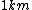 . Ergo, I chose (B). . Ergo, I chose (B).
|
bili
2011-11-03 02:05:35 |
Wow, what a great piece of information about online dating websites. I loved it. Online dating has been my passion and I am sure I will have this opportunity to read more about online dating, dating and dating websites.
Premium " target="_blank">http://www.killerlinkx.com/">Premium Web Directory
|
|  | jonestr
2005-11-12 00:31:59 | a handy value to remember is hc=1240eVnm which can make speed the computation here if you just account for the 4 pi^2
Andresito
2006-03-29 21:37:26 |
I also recommend using quantities in eVs.
You could almost approximate every quantity and work only with orders of magnitude as the answers are given in orders of magnitude.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
