|
GR9277 #72
|
|
|
|
|
Alternate Solutions |
jmason86
2009-09-03 19:19:22 | I did this one by limits and general test taking strategy.
Limits: Q --> finite value as T --> 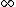 . Eliminates (D) and (E) . Eliminates (D) and (E)
ETS will generally force you to choose between very similar answers. Eliminates (C)
With only (A) and (B) left, it is a good idea to guess. But if you can get a hunch, that is even better. It's probably totally flawed thinking, but I saw the lack of an exponential in the numerator for (B), which made it look similar to a Bose-Einstein distribution. The full expression in (A) reminded me of the Maxwell-Boltzmann distribution that comes from the problem statement. Choose (A)
|  |
|
|
Comments |
ernest21
2019-09-30 05:00:43 | Cool! I\'ll surely be coming back for the next posts from you. You\'re an incredibly engaging writer that I can freely recommend this article to my college students. clash royale best decks |  | BerkeleyEric
2010-09-17 17:04:59 | If you remember that 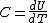 , then immediately you can see that there will have to be the squared sum in the denominator, so only A and B remain. And there still has to be the exponential in the numerator (a derivative won't get rid of that), so the answer must be A. , then immediately you can see that there will have to be the squared sum in the denominator, so only A and B remain. And there still has to be the exponential in the numerator (a derivative won't get rid of that), so the answer must be A.
flyboy621
2010-10-22 16:11:48 |
+1
|
|  | jmason86
2009-09-03 19:19:22 | I did this one by limits and general test taking strategy.
Limits: Q --> finite value as T --> 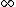 . Eliminates (D) and (E) . Eliminates (D) and (E)
ETS will generally force you to choose between very similar answers. Eliminates (C)
With only (A) and (B) left, it is a good idea to guess. But if you can get a hunch, that is even better. It's probably totally flawed thinking, but I saw the lack of an exponential in the numerator for (B), which made it look similar to a Bose-Einstein distribution. The full expression in (A) reminded me of the Maxwell-Boltzmann distribution that comes from the problem statement. Choose (A)
|  | RebeccaJK42
2007-03-23 10:27:19 | Where does the k in the numerator come from?
alpha
2007-03-30 22:37:37 |
k is Boltzmann constant.. The k on the numerator is actually canceled out by the 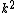 in the denominator in the denominator
|
Richard
2007-09-14 00:05:03 |
The fact of the matter is, you have a factor of
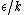 introduced by the derivative. introduced by the derivative.
To make it look pretty, they multiplied the top and bottom by 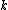 giving (with the extra giving (with the extra  ) the factor ) the factor ^2) . Then of course, you have the . Then of course, you have the 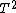 . .
|
|  | Andresito
2006-03-29 10:05:29 | I could not obtain T^2 in the denominator. Is there an error in the solution provided by the ETS?
radicaltyro
2006-10-31 14:19:25 |
Hi Andresito,
Review your calculus and try again. The answer is correct.
|
Blue Quark
2007-11-01 08:00:11 |
Andresito you made the same mistake I did. The T is in the denominator, not the numerator. Thus when you differentiate you get a (-T^(-2)) in front of the exponential in addition to the normal e/k
|
drizzo01
2012-11-08 07:40:44 |
am I the only one who doesn't see a T in the denominator of the second term? I appreciate that T^2 would be in the denominator if there was a T to being with, but as far as I can see, the only T's are within the expression for the exponential, which don't come out upon taking a derivative.
|
drizzo01
2012-11-08 07:46:58 |
wait nvm, got it.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 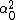 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
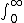 |
| $\partial$ |
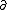 |
| $\Rightarrow$ |
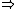 |
| $\ddot{x},\dot{x}$ |
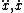 |
| $\sqrt{z}$ |
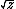 |
| $\langle my \rangle$ |
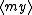 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
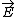 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
