|
GR9277 #100
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
Albert
2009-11-05 04:38:54 | Alternate solution:
No center of mass needed, no torque, no directions, nothing! I solve it by simply taking the ratio of the masses with the lengths of the rod on either side of the fulcrum. And here's how:
On one side you have 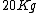 and other side has and other side has 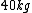 . The rod weighs . The rod weighs 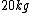 , so I divide , so I divide 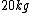 in half and give both weights in half and give both weights 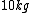 each. And now they weigh each. And now they weigh 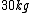 and and 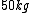 . .
Once reached so far, just put 'em up in ratio and get it,
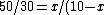)
 comes out comes out 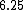 , which is of course , which is of course 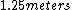 further from the center. further from the center.
The god-damned technique works every freakin' time!
Just make sure you set the ratio to "more mass: lesser length".
apr2010
2010-04-08 15:26:08 |
That is interesting that you do not know which has less length...Keeping the indexes right should work.
|
SurpriseAttachyon
2015-09-10 15:00:03 |
That\'s so strange that this works. The mass on the bar on each side and the mass from the weight on each side should be treated differently because as you move the bar, the bar-mass portion changes but the weight-mass doesn\'t.\r\n\r\nYet when you plug in different answers, it\'s still correct. That\'s odd.
|
nikog
2015-10-20 19:04:27 |
it\'s not that odd. The torque produced from a force F at the a point p at a distance x (i.e at the point x+p) is τ=Fx. Instead if you consider a problem where you have two forces F1=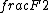 and F2= and F2=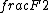 symmetrical to the point p and you measure the torgue at x+p then\r\nτ= symmetrical to the point p and you measure the torgue at x+p then\r\nτ=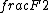 ( l+x) - ( l+x) - 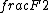 (l-x) = Fx where l the distance from the point p (l-x) = Fx where l the distance from the point p
|
|  | matonski
2009-03-24 01:57:48 | I just put the origin at the center and found the center of mass. COM =  + 40 \text{kg}(5\text{m})}{80\text{kg})
kroner
2009-09-29 14:09:00 |
I think it's safe to say that matonski wins.
|
adjwilley
2009-11-04 10:40:16 |
Beautiful.
|
torturedbabycow
2010-04-09 10:14:17 |
Seconding the "beautiful." In fact, I think I might need a cigarette after reading it. ^__^
|
alemsalem
2010-09-26 09:32:41 |
fuck yeah :) im also gonna smoke now
|
neon37
2010-11-12 09:11:16 |
Damn!......Elegant!...
|
elenaPh
2013-04-15 11:40:16 |
amazing solution ! thanks!
|
aaa2
2014-09-25 12:06:00 |
wow just wow
|
justacomment
2014-10-07 23:19:21 |
Salute.
|
blabla0001
2017-03-25 09:26:30 |
this solution is too good for me. it is also so good that it becomes dangerous. hope i ll never need it again
|
|  | vsravani
2008-11-01 10:51:15 | why is minus sign taken in the equation for 40kg mass
20gd+20gq-40gx=0?
elzoido238
2008-11-06 11:37:44 |
There is a negative sign for the torque due to the 40 kg mass because its contribution to the torque is in the opposite direction of the torques arising from the 20 kg mass and the mass of the rod.
|
|  | Andresito
2006-03-30 13:01:46 | @astro_allison, thank you for the alternative. |  | astro_allison
2005-11-26 23:32:09 | the term "10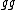 " doesn't make sense to me... " doesn't make sense to me...
I solved it this way:
if 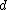 is the distance from the center of mass to the fulcrum, is the distance from the center of mass to the fulcrum,
 = 40(5-d))
solving, you get 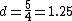
for some reason when I solved it with the 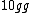 term in your equation, I got term in your equation, I got 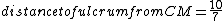
yosun
2005-11-27 02:28:28 |
astro_allison: thanks for the typo-alert; it has been fixed. (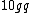 should be should be 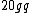 ... note that the first g is a q.) also, thanks for the alternate solution. ... note that the first g is a q.) also, thanks for the alternate solution.
|
gotfork
2008-10-17 11:31:32 |
I'm a bit confused, where does the 20d come from?
|
gotfork
2008-10-17 12:23:09 |
Whoops, just realized the rod has a mass.
|
his dudeness
2010-09-05 16:27:20 |
Yeah I made the same mistake as gotfork... it's tough to get used to things like rods and ropes having masses after so many years of physics :-) ... luckily the answer came out close enough to be right anyway(1.667~1.5)
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
