|
GR8677 #80
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-08-23 12:20:38 | I really appreciate this problem....thanks.... tree service Orlando |  | nakib
2010-04-02 09:01:27 | Don't go for calculating all the answer choices for 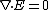 . .
Eliminate C, D ~> Each term has a non-zero contribution to the div. but both terms are +ve, they can't possible cancel each other out.
Eliminate E ~> Just one term that has a non-zero contribution to the div.
Eliminate A ~> Each term has a non-zero contribution to the div. but one term has a factor of 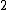 multiplied to it. multiplied to it.
(B) is the correct choice. |  | senatez
2006-10-16 20:25:28 | The electric field must also be a gradient of a function (the potential). Mixed partials of the potential function must be equal. |  |
|
|
Comments |
casseverhart13
2019-08-23 12:20:38 | I really appreciate this problem....thanks.... tree service Orlando |  | nakib
2010-04-02 09:01:27 | Don't go for calculating all the answer choices for 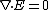 . .
Eliminate C, D ~> Each term has a non-zero contribution to the div. but both terms are +ve, they can't possible cancel each other out.
Eliminate E ~> Just one term that has a non-zero contribution to the div.
Eliminate A ~> Each term has a non-zero contribution to the div. but one term has a factor of 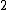 multiplied to it. multiplied to it.
(B) is the correct choice.
neon37
2010-11-04 04:40:24 |
Its not too hard if you think about how to do it fast before hand. It might take longer to think about some other logic. Divergence is a dot product, so for 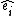 terms you take terms you take 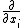 . That shouldnt be too difficult. In this case it was just the second one, so it took me about 7 seconds maximum after reading the question. . That shouldnt be too difficult. In this case it was just the second one, so it took me about 7 seconds maximum after reading the question.
|
|  | senatez
2006-10-16 20:25:28 | The electric field must also be a gradient of a function (the potential). Mixed partials of the potential function must be equal.
student2008
2008-10-12 12:08:08 |
Not necessarily. Since 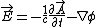 , you're right only in the electrostatic case, which takes place here. And in general we can't get rid of the , you're right only in the electrostatic case, which takes place here. And in general we can't get rid of the  by a gauge transformation, since the condition by a gauge transformation, since the condition 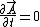 implies implies 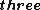 scalar ones. scalar ones.
Although, since there're only 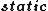 expressions for the electric field, we can infer that the problem expressions for the electric field, we can infer that the problem 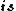 electrostatic. electrostatic.
|
Prologue
2009-11-06 21:03:53 |
You can't infer that it is electrostatic, the curl is nonzero.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
