|
GR8677 #61
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-08-30 03:31:57 | Cool! I\'ll surely be coming back for the next problem from you. custom car Orlando\r\n |  | Herminso
2009-09-21 19:28:34 | Consider the system rocket of mass 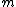 plus a fraction plus a fraction 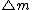 of combustible traveling at velocity of combustible traveling at velocity  just before the just before the 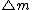 mass is exhausted. From a frame that moves at velocity mass is exhausted. From a frame that moves at velocity  we see the system instantaneously at rest, and then when the mass we see the system instantaneously at rest, and then when the mass 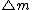 is exhausted, we see that the mass is exhausted, we see that the mass 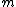 moves front at velocity moves front at velocity  , while , while 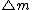 moves backward at moves backward at  that is the speed of rocket's exhaust combustible. By momentum conservation that is the speed of rocket's exhaust combustible. By momentum conservation
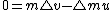  -(\triangle m/\triangle t) u=0) or or -(\partial m/\partial t) u=0) just the equation given since just the equation given since  is negative for the test makers. is negative for the test makers.
Thus  is truly the speed of rocket's exhaust combustible is truly the speed of rocket's exhaust combustible |  | kimseonta
2009-01-07 01:18:00 | Sorry about the one that I posted below...
it is totally incorrect...so I am now going to post the solution again...
The rocket is in a free space -> No external forces
the momentum must be conserved.
Pi=Pf
mv=(m+delta m)(v+ delta v)+(V+v)( - delta m)
, where the delta m should be negative when considering a rocket propulsion. And V is the velocity [Not speed] of the rocket's exhaust from the rocket's frame.
[m + (delta m)](delta v) - V(delta m) = 0
take /(delta t) and limit[delta t -> 0]
Then,
mdv/dt - Vdm/dt = 0
Here, of course, V is negative[vector]. Let u be the speed[scalar] of the rocket's exhaust from the rocket's frame.
 u = -V u = -V
mdv/dt + udm/dt = 0: Here is the answer. |  |
|
|
Comments |
casseverhart13
2019-08-30 03:31:57 | Cool! I\'ll surely be coming back for the next problem from you. custom car Orlando\r\n |  | GPRE
2013-09-24 07:26:28 | Would it be right to look at it like this: The second term suggests a change in mass and the only way the rocket's mass changes is by spending fuel. |  | Almno10
2010-11-11 23:11:14 | If you wanted to fart in space in order to propel yourself forward, you'd have to pull your pants down first so the fart particles wouldn't collide with the seat of your pants.
padkins
2011-02-06 12:44:41 |
I only fart neutrinos
|
|  | subwoofer911
2009-11-03 23:43:34 | v is the speed of the rocket, so A, B and C are automatically wrong. And there IS an acceleration  v/ v/ t, so the constant u cannot be an instantaneous velocity, D. Therefore it is E. t, so the constant u cannot be an instantaneous velocity, D. Therefore it is E.
varsha
2016-02-20 08:30:26 |
Common sense...Nice
|
|  | abacus
2009-10-06 23:39:42 | Rocket equation must remain correct under gallilean symmetry
v -> v+v0
this leaves E |  | Herminso
2009-09-21 19:28:34 | Consider the system rocket of mass 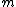 plus a fraction plus a fraction 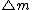 of combustible traveling at velocity of combustible traveling at velocity  just before the just before the 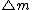 mass is exhausted. From a frame that moves at velocity mass is exhausted. From a frame that moves at velocity  we see the system instantaneously at rest, and then when the mass we see the system instantaneously at rest, and then when the mass 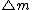 is exhausted, we see that the mass is exhausted, we see that the mass 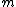 moves front at velocity moves front at velocity  , while , while 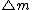 moves backward at moves backward at  that is the speed of rocket's exhaust combustible. By momentum conservation that is the speed of rocket's exhaust combustible. By momentum conservation
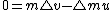  -(\triangle m/\triangle t) u=0) or or -(\partial m/\partial t) u=0) just the equation given since just the equation given since  is negative for the test makers. is negative for the test makers.
Thus  is truly the speed of rocket's exhaust combustible is truly the speed of rocket's exhaust combustible
Quynh_Strange_Beauty
2014-10-13 23:26:50 |
We can quickly see that the meaning of equation is momentum conservation (Delta (mv)_1 - Delta (mv)_2 = 0). That's enough. no more math.
So u must be the speed of the exhaust. (D or E)
OK. What happen if u = 0 ? the equation says rocket gain no momentum. So u must be speed of exhaust relative to rocket. (IF I picked D, my rocket can gain momentum if I choose certain frame of reference, not true)
|
|  | kimseonta
2009-01-07 01:18:00 | Sorry about the one that I posted below...
it is totally incorrect...so I am now going to post the solution again...
The rocket is in a free space -> No external forces
the momentum must be conserved.
Pi=Pf
mv=(m+delta m)(v+ delta v)+(V+v)( - delta m)
, where the delta m should be negative when considering a rocket propulsion. And V is the velocity [Not speed] of the rocket's exhaust from the rocket's frame.
[m + (delta m)](delta v) - V(delta m) = 0
take /(delta t) and limit[delta t -> 0]
Then,
mdv/dt - Vdm/dt = 0
Here, of course, V is negative[vector]. Let u be the speed[scalar] of the rocket's exhaust from the rocket's frame.
 u = -V u = -V
mdv/dt + udm/dt = 0: Here is the answer. |  | kimseonta
2009-01-06 20:13:36 | This is my own way to make the typo (?) clear...
The same idea goes: the conservation of the momentum.
Pi = Pf
mv = (m + dm)(v+dv) + (dm)V, where V <0 of course.
= mv+mdv+vdm+dmdv+(dm)v
Now there exist two appoximations that one can make.
- V >> v : one can simply assume that the speed of the exaust from a rocket should be much faster than the one of the rocket.
-dmvm is almost zero relative to the other parts of the equation.
so the simplified version will be here...
mdv+Vdm=0
m(dv/dt) + V(dm/dt) = 0 |  | Poop Loops
2008-09-24 10:44:52 | I don't get the jump from Line 2 to Line 3. Where does mdV come from? And why is it approx. equal to dm'V?
mv = mv + mdv - dm'v - dm'dv + dm'v - dm'V
Subtract mv from both sides and -dm'v and +dm'v cancel, so you get:
0 = mdv - dm'dv - dm'V
(m - dm')dv = dm'V
So I have no idea how (m - dm')dv relates to mdV
realcomfy
2008-10-31 03:25:25 |
It was stated in the solution that higher order terms such as 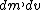 were neglected. The solution thus becomes what is already there were neglected. The solution thus becomes what is already there
|
|  | hefeweizen
2006-11-30 12:10:53 | is there a typo in the last line?
mdv = -Vdm
blue_down_quark
2008-08-27 23:44:48 |
I think V is assumed to be negative in the reference frame where v is positive. It's simply the exhaust velocity without its sign.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 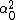 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
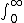 |
| $\partial$ |
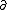 |
| $\Rightarrow$ |
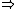 |
| $\ddot{x},\dot{x}$ |
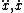 |
| $\sqrt{z}$ |
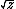 |
| $\langle my \rangle$ |
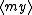 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
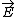 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
