|
GR0177 #97
|
|
|
Problem
|
|
|
This problem is still being typed. |
Optics }Refraction }Refraction
From Snell's Law, one obtains 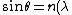 \sin\theta^{'}) , since the index of refraction of air is about 1. , since the index of refraction of air is about 1.
Now, differentiate both sides with respect to  . .
 \sin\theta^{'})\\
0&=& \frac{dn(\lambda)}{d\lambda} \sin\theta^{'}+(n(\lambda) \cos\theta^{'}) \frac{d\theta^{'}}{d\lambda}\\
\delta \theta^{'} &=& |\tan\theta^{'}/n \frac{dn(\lambda)}{d\lambda} \delta \lambda|, <br />
\end{eqnarray})
which gives choice (E) to be the angular spread.
This solution is due to ShyamSunder Regunathan.
|
|
|
Alternate Solutions |
jsdillon
2008-04-07 20:27:09 | This problem can be solved using the limiting case of  =0. =0.
We also know that 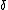  ' must go to 0 at ' must go to 0 at  =0 since normally incident rays don't refract (think Snell's Law with =0 since normally incident rays don't refract (think Snell's Law with  =0). That leaves only (E), the correct answer. (D) doesn't work because as =0). That leaves only (E), the correct answer. (D) doesn't work because as  goes to 0, goes to 0,  ' also goes to 0. ' also goes to 0.
(I thought, since I'm now almost all the way through all four tests with the exam now 6 days away, that I'd leave a small contribution. Thanks Yosun!) |  |
|
|
Comments |
f
2019-10-15 21:12:02 | Il a remporté deux antennes, achevés depuis plus de 80 pour cent de ses passes et a fait deux passes clés, y compris son assist.\r\nf http://www.lindbaek.eu/tobuyes13.asp |  | solidstate
2011-11-05 22:43:21 | TRICK TRICK: only E has right unit.
Yurlungur
2012-04-08 20:04:32 |
Actually (B), (D) and (E) are unitless. However, eliminating (A) and (C) this way is nice. :)
|
msdec
2016-09-08 04:33:49 |
Yes but only E is in the proper units of radians.
|
|  | mistaj
2011-08-24 08:35:17 | You can eliminate all but B and E by noting ) needs to be part of the final solution. This is the case because if n = 1 for all wavelengths, the solution would be 0 since the angular spread is constant. Now note, that the transmitted angle and the incident index of refraction is only in E. Since n will impact our final answer (imagine if both needs to be part of the final solution. This is the case because if n = 1 for all wavelengths, the solution would be 0 since the angular spread is constant. Now note, that the transmitted angle and the incident index of refraction is only in E. Since n will impact our final answer (imagine if both ) and n are the same - there will be no refraction), the only complete answer is E. and n are the same - there will be no refraction), the only complete answer is E. |  | bluelight
2011-02-24 20:38:07 | i like Yosun's solution but how does the last step come about? can sombody explain it?
Da Broglie
2011-04-08 17:04:12 |
In the last step Yosun moved cos(\theta)^\prime \frac{d\theta^\prime}{d\lambda}) to the left side of the equal sign and divided through by to the left side of the equal sign and divided through by cos(\theta)^\prime) converting converting ^\prime}{cos(\theta)^\prime}) to to ^\prime) . Multiply through by . Multiply through by 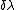 to solve for to solve for 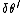 . .
|
|  | barson
2009-10-18 04:39:38 | How to define the theta which depends on lamda?
I got some confuse about this. |  | realcomfy
2008-10-24 14:16:00 | Just curious, but how does the ) turn into just plain turn into just plain  in that final solution? in that final solution?
nobel
2008-11-01 07:34:16 |
n(lambda) implies n is a function of lambda. its not
n *lambda
|
|  | jsdillon
2008-04-07 20:27:09 | This problem can be solved using the limiting case of  =0. =0.
We also know that 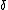  ' must go to 0 at ' must go to 0 at  =0 since normally incident rays don't refract (think Snell's Law with =0 since normally incident rays don't refract (think Snell's Law with  =0). That leaves only (E), the correct answer. (D) doesn't work because as =0). That leaves only (E), the correct answer. (D) doesn't work because as  goes to 0, goes to 0,  ' also goes to 0. ' also goes to 0.
(I thought, since I'm now almost all the way through all four tests with the exam now 6 days away, that I'd leave a small contribution. Thanks Yosun!)
Daw6
2009-11-05 10:43:05 |
We can also think about the limiting case n( )=1, i.e. no change in medium is taking place. In this case, )=1, i.e. no change in medium is taking place. In this case,   '= 0 also. The only two choices that provide this contain a factor of dn/d '= 0 also. The only two choices that provide this contain a factor of dn/d , and only (E) provides the aforementioned limiting case as well. , and only (E) provides the aforementioned limiting case as well.
Just a thought.
|
apr2010
2010-04-09 16:56:08 |
Following your argumentation, D is possible.
I would just say, as Snells law contains also 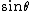 choose D over E. choose D over E.
|
Yurlungur
2012-04-08 20:11:40 |
I think this is the best solution.
|
|  | Mexicana
2007-10-02 18:23:52 | Another funky way of doing this (somehow less abstractly than yosun) is to use the general formula for combination of errors which would give for this case ^2=(\frac{\partial \theta'}{\partial\lambda})^2(\delta\lambda)^2) . Then you just need to get . Then you just need to get ^2) using Snell's Law. Whenever you see the word 'spread' or 'uncertainty' or just 'error', always remember the pretty formula for combination of errors! using Snell's Law. Whenever you see the word 'spread' or 'uncertainty' or just 'error', always remember the pretty formula for combination of errors!
Richard
2007-10-30 22:20:00 |
Personally, I find this to be more correct.
There seems to be a bit of hand-waving in dear Yosun's quoted solution. In particular, I am thinking of the last step.
|
|  | scottopoly
2006-10-29 23:57:28 | Really minor, but the problem says it's in a vacuum, so your comment that it's in air is incorrect. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
