GREPhysics.NET: GR0177 #73

GR0177 #73

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Mechanics $\Rightarrow$ }Forces

The net force of the system is $\sum F = (m_a+m_b) a$ , and thus the net acceleration due to this force is $a = F/(m_a+m_b)$ .

The net force for mass A is just $m_a a = F - F_{ab}$ . By Newton's Third Law, $F_{ab}=N$ is just the normal force exerted by A on B.

Solving for the normal force, one finds that $N = F - m_a a = F(1 - m_a/(m_a+m_b))=F(m_b/(m_a+m_b))$ .

Summing up the vertical forces on mass B, and using the fact that the frictional force is just $f=\mu N$ , one finds that $\sum F_y = \mu N-m_b g=0$ for the applied force to balance its mass completely. Thus, $F= (m_a+m_b)g/\mu$ , which is approximately 400N, as in choice (D) after plugging in the numbers.

Alternate Solutions

ilikefluids 2017-07-09 15:44:05	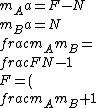$m_A a = F - N \\\\ m_B a = N \\\\ \\frac{m_A}{m_B} = \\frac{F}{N} - 1 \\\\ F = (\\frac{m_A}{m_B} + 1)N \\\\ \\\\ \\textrm{All of these quantities are easy to calculate;} \\\\ \\frac{m_A}{m_B}=16/4=4, \\\\\\mu N = m_B g \\Rightarrow N = \\frac{m_B g}{\\mu} = \\frac{(4)(10)}{0.5} = 80 \\\\ \\textrm{Hence, }F = 5(80) = 400, \\textrm{ choice (D)}$ Reply to this comment
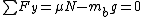
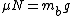
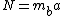
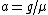
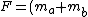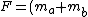R0BB23 2008-06-30 08:46:19	$\sum F_y = \mu N-m_b g=0$ $\mu N=m_b g$ $N=m_b a$ $a=g/\mu$ $F=(m_a+m_b)a$ $F=(m_a+m_b)g/\mu$ Reply to this comment

Comments

ilikefluids
2017-07-09 15:44:05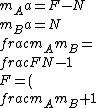

$m_A a = F - N \\\\ m_B a = N \\\\ \\frac{m_A}{m_B} = \\frac{F}{N} - 1 \\\\ F = (\\frac{m_A}{m_B} + 1)N \\\\ \\\\ \\textrm{All of these quantities are easy to calculate;} \\\\ \\frac{m_A}{m_B}=16/4=4, \\\\\\mu N = m_B g \\Rightarrow N = \\frac{m_B g}{\\mu} = \\frac{(4)(10)}{0.5} = 80 \\\\ \\textrm{Hence, }F = 5(80) = 400, \\textrm{ choice (D)}$

Reply to this comment

asdfuogh
2011-11-09 18:09:11

So, you can figure out the normal force pretty quickly to be 80 N. Then you flip your head around and imagine the second block to be accelerated by the normal force due to the first block, which would give the acceleration to be 80N/4 kg = 20 m/s^2. Then you realize that the blocks are moving at the acceleration because there is a normal force between them, so the whole force on the system is a*total_mass = 20 m/s^2 * 20 kg = 400 N.

:( Too bad this isn't the kind of stuff you can come up with under pressure... I kept messing up the calculations when I was doing this as a practice test :(.

Reply to this comment

Dodobird
2010-11-01 08:50:49

Use the principle of equivalence. Coefficient of static friction gives us one part of vertical force for every two parts of horizontal force. We need 40 N of vertical force, therefore we need 80 N of horizontal force on B. Because we have to push the entire system, we need five times this force, which is 400 N. Answer = D

Reply to this comment

carl_the_sagan
2008-11-07 22:05:17

I'm not sure if this is a valid way to tackle the problem but it's how my messed up line of thinking went:

The block B needs to be pushed up equal to the force gravity exerts on it to stay in place. Take gravity to be 10m/s^2 for convenience and it needs 40N.

However, the coefficient of friction is only .5, so you have to push twice as hard, so 80N. This means you need to accelerate B by 80N/4kg = 20m/s^2 horizontally to produce enough "lift" to balance things. Since the entire system is 20kg, F = 20kg*20m/s^2 = 400N

bert
2009-11-06 11:15:06

I like this solution. These problems should be solved with quick logic, not tedious math and equations whenever possible. :)

solidstate
2011-11-04 22:05:52

This works pretty fine.

Reply to this comment

R0BB23
2008-06-30 08:46:19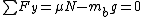

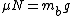
$\sum F_y = \mu N-m_b g=0$
$\mu N=m_b g$
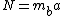
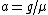
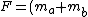$N=m_b a$
$a=g/\mu$
$F=(m_a+m_b)a$
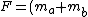$F=(m_a+m_b)g/\mu$

N
2011-04-07 20:55:31

To clarify RoBB23's solution: the important point to recognize here is that the horizontal force on the two blocks is not the same, but that they accelerate at the same rate: $a_x^A$ = $a_x^B$ . Then it's just the normal stuff.

John777
2011-11-07 10:45:40

Good Job!

QuantumCat
2014-09-22 17:19:18

Fast and efficient. Love it!

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone