|
GR0177 #65
|
|
|
Problem
|
|
|
This problem is still being typed. |
Statistical Mechanics }Approximations }Approximations
At high temperatures, one has 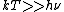 . .
One expands the argument of the denominator according to 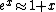 (for small x). The denominator becomes (for small x). The denominator becomes =h\nu/kT) . Since the whole quantity of the denominator is squared, the top . Since the whole quantity of the denominator is squared, the top ^2) term is canceled. term is canceled.
In the numerator, one has 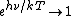 , since , since 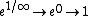 . .
Thus, one arrives at choice (D).
One either remembers this fact about solid or one derives it, as shown above. (Also, for low temperatures, at say around 20K for most solids, the Debye 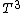 law applies, and specific heat is proportional to law applies, and specific heat is proportional to 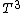 . One can't find this result from the Einstein formula, which is why Debye's theory is more accurate for solids.) . One can't find this result from the Einstein formula, which is why Debye's theory is more accurate for solids.)
|
|
|
Alternate Solutions |
atomike238
2011-02-05 16:44:56 | Use L'H˘pital's rule.
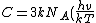^2\frac{e^{hv/kT}}{(e^{hv/kT}-1)^2})
Let 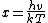 and and = x^2e^x)
Since 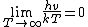
then using L'H˘pital's rule, =\lim_{x\to\0}\frac{d(x^2e^x)}{d(e^x-1)^2})
Product rule on the top and chain rule on the bottom yield
=\lim_{x\to\0}\frac{x^2e^x+ 2xe^x}{2(e^x-1)e^x}=\lim_{x\to\0}\frac{x^2+ 2x}{2(e^x-1)})
Use L'H˘pital's rule one more time
=\lim_{x\to\0}\frac{2x+2}{2e^x}=\frac{x+1}{e^x}=\frac{0+1}{e^o}=1)
Since 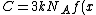) then then
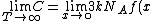 = 3kN_A) (Choice D) (Choice D)
|  |
|
|
Comments |
atomike238
2011-02-05 16:44:56 | Use L'H˘pital's rule.
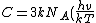^2\frac{e^{hv/kT}}{(e^{hv/kT}-1)^2})
Let 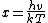 and and = x^2e^x)
Since 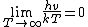
then using L'H˘pital's rule, =\lim_{x\to\0}\frac{d(x^2e^x)}{d(e^x-1)^2})
Product rule on the top and chain rule on the bottom yield
=\lim_{x\to\0}\frac{x^2e^x+ 2xe^x}{2(e^x-1)e^x}=\lim_{x\to\0}\frac{x^2+ 2x}{2(e^x-1)})
Use L'H˘pital's rule one more time
=\lim_{x\to\0}\frac{2x+2}{2e^x}=\frac{x+1}{e^x}=\frac{0+1}{e^o}=1)
Since 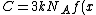) then then
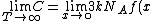 = 3kN_A) (Choice D) (Choice D)
|  | davidkaleko
2010-09-15 14:16:01 | Another quick way to do this: the specific heat certainly isn't going to depend on the frequency of oscillations, so B, C, and E are out. Also, it goes to 0 at T approaches 0, so it's not going to approach 0 as T approaches infinity. This leaves D. |  | jmason86
2009-07-09 23:12:52 | Yosun (or anyone),
In the denominator, you Taylor expand the 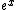 as as 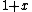 but in the numerator you expand the same but in the numerator you expand the same 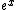 term out to only one order (i.e. =1). Are you allowed to do that? I'm definitely not a proponent of mathematical formalism (what physicist is... especially one taking this damn test), but I wanted to make sure that this sort of thing is generally okay... to expand the same thing to different orders. term out to only one order (i.e. =1). Are you allowed to do that? I'm definitely not a proponent of mathematical formalism (what physicist is... especially one taking this damn test), but I wanted to make sure that this sort of thing is generally okay... to expand the same thing to different orders.
Thanks!!
Shadow
2010-11-10 22:55:04 |
He did expand the numerator, but as T becomes large, the x term goes to zero, which leaves you with 1 on the numerator.
|
|  | Simplicio
2009-03-25 12:14:00 | A very fast way to answer this is to know that both Einstein's and Debye's theory tends to the classical limit when T is large, so (D) is the obvious answer.
But even if you forgot what the classical limit is, one should remember h only exist in the quantum regime, so any solution in the classical high T limit cannot have h which leaves us with (A) and (D). And hopefully at this point C=zero can be elimnated. |  | petr1243
2008-03-18 12:05:16 | Debye and Einstein's formulas of heat capacity for low T and high T both reduce to 3R , which is the classic rule of Dulong and Petit. |  | Jeremy
2007-10-25 12:25:56 | An Einstein solid is nothing more than a 3D harmonic oscillator, which equipartition (high temperature limit) says will have 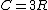 . .
Another aside - answer choices (C) and (E) do not have the correct units. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
