|
GR0177 #54
|
|
|
|
|
Alternate Solutions |
ramparts
2009-10-08 10:53:17 | Better yet, it's one triangle :P 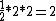 kg m/s. kg m/s. |  |
|
|
Comments |
kevintah
2015-10-02 10:29:02 | I mean . . . . when you look at it, it just screams area under the curve scenario. . . so you just do area of triangle. |  | Almno10
2010-11-09 12:57:21 | better yet, you can write the equations of the lines F = 2t on [0,1] and F = -t+4 on [1,2] and simply sum the integrals! j/k
Dr. D.R. Dopetec
2011-09-28 19:38:06 |
ha yes
|
|  | fiber
2009-11-05 22:09:52 | better yet, put the triangles together and it's one rectange with 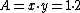 |  | ramparts
2009-10-08 10:53:17 | Better yet, it's one triangle :P 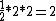 kg m/s. kg m/s. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces 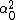 . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
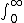 |
| $\partial$ |
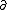 |
| $\Rightarrow$ |
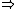 |
| $\ddot{x},\dot{x}$ |
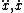 |
| $\sqrt{z}$ |
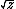 |
| $\langle my \rangle$ |
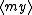 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
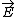 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
