|
GR0177 #49
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
duckduck_85
2008-10-30 22:44:09 | I think it might be important to note that ETS is using the term "Maxwell-Boltzmann distribution" indistinctively from "Canonical Distribution" in this problem. Even though they do have the same mathematical form, i think it might be more appropriate to refer to this system as a system following a canonical distribution.
thatoneguy
2011-11-08 05:46:49 |
Old comment, but I don't think that's necessarily true. The Canonical Distribution doesn't have degeneracies. IIRC, it's of the form Z = 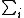  . In particular, the distribution for an MB system can have degeneracies, unlike those systems which follow Fermi-Dirac statistics (which still follow the Canonical Distribution function. I believe they are using "Maxwell-Boltzmann Distribution" distinctively in this case. . In particular, the distribution for an MB system can have degeneracies, unlike those systems which follow Fermi-Dirac statistics (which still follow the Canonical Distribution function. I believe they are using "Maxwell-Boltzmann Distribution" distinctively in this case.
|
4elesta
2012-04-15 15:23:49 |
Please, can someone explain, why it's said that distribution is Maxwellian? thanks)
|
ETScustomer
2017-10-10 18:53:57 |
Maxwell also did great thermal work.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
