shka
2018-07-06 00:08:13 | The fraction of rays/particles detected is proportional to the solid angle subtended by the detector, so the ratio of the fractions of particles detected is equal to the ratios of the solid angles: F2 / F1 = S2 / S1. When the source is next to the detector, the solid angle is 2*Pi, since the solid angle of a whole sphere is 4*Pi, and half the rays are detected (F1 = 1/2). The formula for solid angle S is S = A / r^2 , where A is the area of the patch of sphere of radius r subtended by S. To find S2, let r = 1 meter. Since 1 meter is much larger than the radius of the detector face ( d/2 = 4 cm ), the patch of sphere subtended by S2 is almost flat, so we can use A = Pi * (d/2)^2 = 16 Pi cm^2. Thus S2 = 16 * Pi * 10^-4. Thus S2 / S1 = 8 * 10^-4. Multiplying this by F1 gives F2 = 4 * 10^-4, choice C. |  |
amirhse
2016-09-24 14:51:26 | See: https://en.wikipedia.org/wiki/Inverse-square_law,\r\nfor spherical waves:\r\n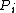 = =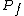 where P is power,so\r\n where P is power,so\r\n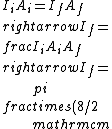^2}{4\\times\\pi\\times(1\\mathrm{m})^2}=4\\times 10^{-4} \\times I_i) |  |
YHS
2013-09-15 09:12:49 | One may use the solid angle to solve this problem.
Imagine the cone which the top is on a point source and the base plane is a detector. Let the solid angle we want to get be s. Then
s= 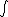 dΩ dΩ
= $\int _0 ^\2π$ dφ $\int_0^\θ$ sinθdθ
=2π(1-cosθ)
cosθ = (1+0.04^2)^(-1/2) ≒ 1 - 8*10^-4, (approximation with binomial expansion) so
s = 16π*10^-4
The fraction is
$\frac{16π*10^-4}{4π}$ = 4*10^-4 |  |
walczyk
2012-10-18 14:06:37 | Not sure why this hasn't been said but the flux is equal in all directions so a meter away 100% of the flux leaves through a sphere of radius 1m, and the detector can only detect the fraction of the sphere that it is in front of. The question is asking what fraction of the surface area of the sphere does the detector intersect with? |  |
deafmutemouse
2012-10-05 14:39:18 | Not sure if I just got lucky with the math, but the way I thought of it was to take a ratio of volumes. My thought was that we essentially have a certain amount of "stuff" that is radiated outward from a point source. The volume that this stuff is radiated through is a sphere of radius 1m. 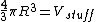
Picture the detector's circular face at the edge of this sphere, so that if you were to trace a line from the center of the sphere to the edge of the circular face, you'd outline the edge of a cone. 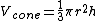 (the volume of stuff detected). (the volume of stuff detected).
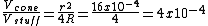 , as in C. , as in C.
walczyk
2012-10-18 14:00:19 |
It is much easier to visual a unit sphere, and a circle of radius 8cm and divide there area of the circle by the surface area of the sphere.
|
|  |
bosonichadron2
2011-05-31 13:19:15 | Correct me if I'm wrong, but I feel like I'm taking crazy pills here.
The question states:
"...50% of all emitted gamma rays...are detected. If the dectector is moved to 1 m away, the fraction of detected gamma rays drops to [choices] "
Now, it may be (and probably is) that they didn't mean for the 50% thing to mean anything more than showing that the efficiency of the detector is 100%.
But the fact of the matter is that the question can be more readily understood to mean that they are asking us to give the fraction of total gamma rays emitted and not the fraction of the initial detected. They don't really specify which "fraction" they are asking us to calculate, but it is only natural to read the phrase " the fraction of detected gamma rays" to mean the same fraction mentioned in the previous sentence (i.e. the fraction of the total emitted).
Furthermore, even if one did realize this ambiguity there would be no way to tell which they are talking about since both "fractions" are possible answers which makes process of elimination impossible. At best this question is poorly worded, and at worst is very misleading.
alece
2016-10-23 00:32:17 |
I agree. The wording was very misleading, and I was not sure which ratio they were asking for.
|
|  |
jumbocrab
2010-11-10 12:23:04 | the point souse radiates in all directions so it will form a sphere of radiation where anything intersecting that sphere will be hit by the radiation. The detector has a cross sectional area of pi*r^2 so the detector will intersect or "cut" through the sphere. The surface area of the sphere is 4*pi*R^2 so to find the amount of radiation detected, we just have the radio of areas. Cross-sectional area of detector / surface area of sphere of radiation where r = d/2 = 0.04m and R = 1m
jordan_taylor
2014-10-22 17:32:25 |
Why is it when I apply this to the initial situation, where the source is near the detector, (Acircle/Asphere) I get .25 and not .5 as the question states?
|
|  |
BerkeleyEric
2010-07-11 18:45:57 | From geometry we know that the percentage of gamma rays detected is linearly proportional to the solid angle.
The solid angle for the far-away source is A/R^2 and the solid angle for the close-source is (by symmetry) 2 pi. Taking the ratio and multiplying by 50% gives choice (C). |  |
MuffinSpawn
2009-07-16 09:56:35 | I'm thinking of this as simply a diminishing intensity problem. The 50% detected is a red herring I think. It just says that the detector is 100% efficient, but initially approximating the detector is an infinite plane only half of the particles will hit it.
So the fractional intensity is 1 (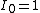 ), and then the intensity at ), and then the intensity at 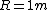 is just is just 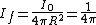 . .
The fraction of particles that hit the front of the detector is then 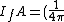 (16\pi \times 10^{-4} m)=4 \times 10^{-4}) . .
chemicalsoul
2009-10-28 08:41:04 |
This is a the best answer!
|
|  |
Ethan
2008-10-10 15:22:06 | I don't know if this adds, but it clarifies the disagreement:
The exact answer is given by the solid angle subtended on the sphere ie ) over the total area over the total area 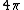 . For our case this is approximatelly the area of the detector and so the approximation is fine. . For our case this is approximatelly the area of the detector and so the approximation is fine. |  |
Anastomosis
2008-04-10 12:33:33 | I guess this really isn't an "alternate" solution, but I just set up a quick ratio, as ratios are among the fastest methods of solving problems, especially on this test.
This is going to be basically the same exact thing as the solution above, just a little easier to follow, I think.
Quick ratios:
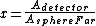
and:
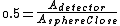
These ratios just say that the fraction of gamma-rays that are detected is going to be the ratio of area of the detector to the total area (of a sphere with the same radius as the distance to the detector).
So, quickly divide the first by the second, the 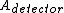 cancels out, and you are left with: cancels out, and you are left with:
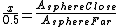
And what is the area of the close sphere? We know that it's just double the area of the detector ^2) , since when it is at that distance, it catches 50% of the gammas. (I just thought of the detector at this distance as a hemisphere, half enveloping the radioactive sample). , since when it is at that distance, it catches 50% of the gammas. (I just thought of the detector at this distance as a hemisphere, half enveloping the radioactive sample).
So:
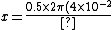^2}{4\pi (1)^2})
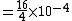
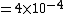
|  |
cedric_tsui
2007-10-30 14:39:33 | I agree that the solution is flawed. The math is correct, but for the wrong reasons.rnrnFirst. One must realize that 50% of the gamma rays are detected when the source is placed against the side of the detector tells us that the detector efficiency is 100%. That is, that every ray that so much as glances the face of the detector is counted. Thus the length of the detector is not important, as the radiation source can only 'see' the circular face.rnrnSecond. The detector is now 1m away from the source. Thus the fraction of the rays it detects is equal to the fraction of rays striking it, which is equal to the surface area of the circular face divided by the surface area of a sphere with a 1m radius.
cedric_tsui
2007-10-30 14:40:52 |
Ung. It killed my formatting.
I agree that the solution is flawed. The math is correct, but for the wrong reasons.
First. One must realize that 50% of the gamma rays are detected when the source is placed against the side of the detector tells us that the detector efficiency is 100%. That is, that every ray that so much as glances the face of the detector is counted. Thus the length of the detector is not important, as the radiation source can only 'see' the circular face.
Second. The detector is now 1m away from the source. Thus the fraction of the rays it detects is equal to the fraction of rays striking it, which is equal to the surface area of the circular face divided by the surface area of a sphere with a 1m radius.
|
sidharthsp
2008-10-21 01:14:46 |
I second that, that is the best explanation. that 50 % thing is a distraction or as "cedric_tsui" says a measure of efficiency of detector...
-Sid
|
gravity
2010-11-09 23:13:47 |
To clarify, I think he meant the surface area of the detector face divided by the surface area of half of a sphere. You can imagine the sample is shooting off gamma rays in every direction - when the detector is up close to it, it picks up half, every gamma ray shot off the right (right side is arbitrary, could be left). Back it up, and you have the same 50% of the gamma rays going through the half sphere of 1m, with the detector taking up 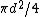 of that area. of that area.
|
|  |
kostas_zarganis
2007-01-11 05:18:46 | À =3.14... |  |
kostas_zarganis
2007-01-11 05:16:26 | I have to show an easier way to find the solution.... Initially for a distance of the source s=1m we have a sphere's volume (4Às^2)/3=4À/3 m^3
The radiation that is detectable in that case is related with the volyme of a cone with base:the cross section of the detector and height h the distance between the source and the detector (h = s = 1m). The volume of the come is:1/3*Àr^2*h (r = 0.04 m)=(16/3) À 10^-4 m^3.
The fraction is the: (volume of the cone)/ (volume of the sphere)=4*10^-4 |  |
freeform
2006-12-01 23:32:48 | It's all about solid angles. (see wikipedia:steradians). Think of the source as an isotropically emitting pt source. With source directly in front of detector, half of all emissions captured by detector as stated in problem. 1 meter away, the fraction is simply area of disk / area of sphere of radius R. |  |
backyard
2006-10-24 06:19:27 | I think the real answer should be 50 percent of that given by choice(c)
julio
2006-11-03 02:10:04 |
backyard : No I don't think so.
50 percents of all emitted gamma rays are detected in the first case because de detector doesn't dectect the rays that go in the opposit direction.
But for the second case, Jon Jockers' solution is rigorous.
|
dirichlet
2006-11-14 11:49:55 |
The solution was absolutely faulty. As the distance from the source i.e. the radius of the sphere is large compared to the diameter it produces a good result. In fact we should have worked with a particular zone of the sphere whose sagitta will be given by the formula
h=\0.5{sqrt{R^2+d^2/4}-R}/\sqrt{R^2+d^2/4}.
From this we can find the area of the required spherical zone via A=2\pi*R*h. And then dividing it by 4\pi*R^2 we get the required result which is now as I can see 3.992*10^(-4). mathbeautymobius@yahoo.com
|
KarstenChu
2007-03-22 13:36:37 |
Yes, Jon Jocker's solution *happens* to work out because the distance the detector is away from the source is large compared to the diameter of the source. In this limit we can take the area of the opening to be almost equal to the fraction of the surface area of the sphere that represents where all the radiation is going.
My point is just to take his solution with a grain of salt.
|
calcuttj
2014-09-22 06:37:08 |
In hindsight, it seems the 50% detection in the first case is there to show that the source emits in all directions (half goes through the circular face because it's so close, the other half is going away from the face) - other than that it's information that is more or less useless (in my mind at least).
The real point of the problem is to realize the source radiates into an area of 4 R^2, and the detector is only R^2, and the detector is only  d^2/4 d^2/4 R^2 of this area. R^2 of this area.
|
calcuttj
2014-09-22 06:39:32 |
My mistake: it should say ( d^2/4)/4 d^2/4)/4 R^2 R^2
|
|  |
