|
GR0177 #13
|
|
|
Problem
|
|
|
This problem is still being typed. |
Optics }Aperture Formula
The circular aperture formula (a.k.a. Rayleigh Criterion) is given by 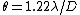 . Plug in the given quantities to get that.
(It's a nice formula to memorize, as it's used as common sense in a variety of engineering fields, as well as in remote-sensing, such as satellite-communications.)
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
kevintah
2015-10-07 05:43:54 | Can anyone tell me where the 1.22 comes from? I would memorize the formula with that constant, but I am just interested to know where it comes from.
NervousWreck
2017-03-28 09:21:55 |
From some accurate integration for a diffraction from a circular aperture
|
poopterium
2017-10-26 00:47:57 |
Just in case anyone comes across this....it comes from integrating over a circular aperture in optics. The 1.22 comes from a zero of a first order Bessel\'s function of the first kind. I believe the zero of the function is about 3.9, then dividing it by pi gives you the 1.22.
|
|  | grae313
2007-11-01 16:19:02 | "that" being 2.5 cm, or choice (B) :) thanks Yosun
ebykl
2008-09-23 21:13:33 |
I'm confused about units...which unit do we have to use as wavelength, do we need to use nanometer or sth else??
|
nobel
2008-10-31 04:40:39 |
use lambda in metres then u get D in metres, use lambda in cms to get D in cms.
1 nanometre is 10^(-7) cm and 10^(-9) m
|
andrew0387
2009-09-30 21:30:14 |
1 nm is 10^(-11) cm. I believe nobel meant to say that 100 nm is 10^(-7)m. Then when dividing by the angle in radians, you get 2.44*10^(-2)m, which is 2.44 cm.
|
Albert
2009-10-27 10:47:29 |
Sorry andrew0387, you seem to be confused. Nobel is right, 1 nm is 10^(-9)m and it is also 10^(-7)cm....always remember whenever you consider smaller units, the number in the power gets bigger. In this case, -7 is bigger than -9. Therefore, 1 nm is NOT 10^(-11)cm.
You may not check the website, I am writing for everyone.
|
| |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  .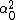
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
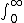| $\partial$ |
 |
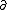| $\Rightarrow$ |
|
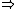| $\ddot{x},\dot{x}$ |
 |
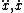| $\sqrt{z}$ |
 |
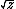| $\langle my \rangle$ |
 |
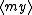| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
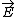| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
